보물 찾기 - 문제

H \times W

의 크기의 그라운드가 있다. 이 그라운드에는 보물이 숨겨져 있는데, 위에서부터

i

행, 왼쪽에서부터

j

열에 있는 칸

X_{i, j}

에는 숨겨져 있는 보물의 수가 적혀져 있다.

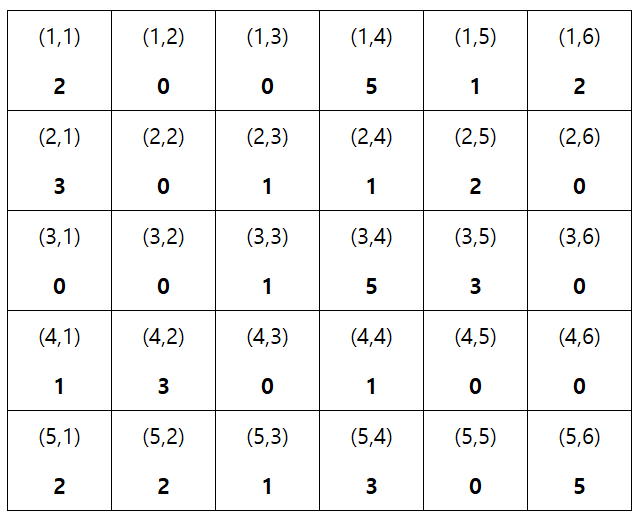
보물 사냥꾼인 판다는 왼쪽 위

(A_{i}, B_{j})

, 오른쪽 아래

(C_{i}, D_{j})

으로 표현되는 사각형 영역

Q

개에 대한 정보를 얻었다.

이 영역은 보물이 묻혀있을 가능성이 높은 정보로 그 중 하나만 골라 채굴을 할 수 있다.
가장 많은 보물이 묻혀있는 영역의 번호를 찾아 판다에게 알려주자.

H

W

Q

X_{1, 1}

X_{1, 2}

...

X_{1, W}

...

X_{H, 1}

X_{H, 2}

...

X_{H, W}

A_{1}

B_{1}

C_{1}

D_{1}

...

A_{Q}

B_{Q}

C_{Q}

D_{Q}

1 \leq H, W \leq 1, 500

1 \leq Q \leq 100, 000

0 \leq X_{i, j} \leq 9

1 \leq A_{i} \leq C_{i} \leq H

1 \leq B_{i} \leq D_{i} \leq W

가장 많은 보물이 묻혀있는 영역의 번호를 출력한다. 첫번째 입력되는 영역의 번호는

1

이며 마지막 영역의 번호는

Q

이다.

5 6 2
2 0 0 5 1 2
3 0 1 1 2 0
0 0 1 5 3 0
1 3 0 1 0 0
2 2 1 3 0 5
2 2 4 5
1 1 5 5

	작성자	제목(댓글)
글이 없습니다.