4098: 기동이 많은 하노이 탑
[만든사람 : ]
문제 설명
하노이 타워는 \(n\)개의 원판과 \(3\)개의 기둥으로 구성되어 있으며, 가장 왼쪽의 기둥에 위치한 \(n\)개의 원판을 가장 오른쪽 기둥으로 다음 규칙을 지키면서 최소 이동 횟수로 옮기는 게임이다.
한 번에 하나의 원판만 옮길 수 있다.
작은 원판 위에 큰 원판을 옮길 수 없다.
하노이 타워는 다양한 변형 문제들이 존재한다. 이 문제는 하노이 타워의 기둥을 \(n\)개로 늘리고 기둥 간에 원판을 옮기기 위한 비용을 정한다. 즉, 각 기둥들 사이의 관계가 그래프의 형태로 구성되며 각 기둥 간에 원판을 옮기는 비용은 인접 행렬의 형태로 주어진다.
원판을 옮길 때에는 기둥과 연결된 기둥으로만 옮길 수 있다. 예를 들어 다음은 기둥이 \(3\)개 있고 각 기둥 간 가중치가 \(1\)인 예를 나타낸다.
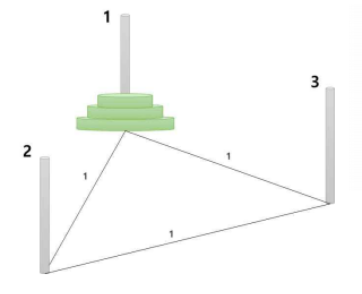
이 경우 \(1\)번 기둥에서 \(3\)번 기둥으로 옮기려면 다음과 같은 과정을 거쳐야 한다.
- 가장 작은 원판을 \(1\)에서 \(3\)으로 옮긴다. (누적 가중치: \(1\))
- 두 번째 작은 원판을 \(1\)에서 \(2\)로 옮긴다. (누적가중치: \(2\))
- 가장 작은 원판을 \(3\)에서 \(2\)로 옮긴다. (누적 가중치: \(3\))
- 가장 큰 원판을 \(1\)에서 \(3\)으로 옮긴다. (누적 가중치: \(4\))
- 가장 작은 원판을 \(2\)에서 \(1\)로 옮긴다. (누적 가중치: \(5\))
- 두 번째 작은 원판을 \(2\)에서 \(3\)으로 옮긴다. (누적 가중치: \(6\))
- 가장 작은 원판을 \(1\)에서 \(3\)으로 옮긴다. (누적 가중치: \(7\))
이와 같은 방법으로 옮기면 \(7\)의 가중치로 \(3\)개의 원판을 \(1\)에서 \(3\)으로 옮길 수 있다. 이보다 더 적은 가중치로 모두 옮길 수 있는 방법은 없으므로 답은 \(7\)이다.
각 기둥의 관계와 출발 기둥과 도착 기둥이 차례로 주어질 때, 출발 기둥에 있는 3개의 원판을 위 규칙 1, 2를 지켜가면서 도착 기둥으로 옮기는 최소 가중치를 구하는 프로그램을 작성하시오.
*다음과 같은 확장 하노이 타워가 주어질 수도 있다.
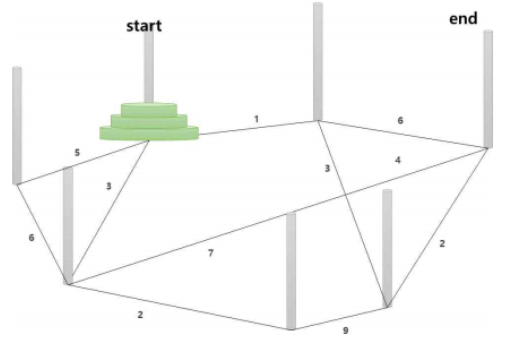
한 번에 하나의 원판만 옮길 수 있다.
작은 원판 위에 큰 원판을 옮길 수 없다.
하노이 타워는 다양한 변형 문제들이 존재한다. 이 문제는 하노이 타워의 기둥을 \(n\)개로 늘리고 기둥 간에 원판을 옮기기 위한 비용을 정한다. 즉, 각 기둥들 사이의 관계가 그래프의 형태로 구성되며 각 기둥 간에 원판을 옮기는 비용은 인접 행렬의 형태로 주어진다.
원판을 옮길 때에는 기둥과 연결된 기둥으로만 옮길 수 있다. 예를 들어 다음은 기둥이 \(3\)개 있고 각 기둥 간 가중치가 \(1\)인 예를 나타낸다.

이 경우 \(1\)번 기둥에서 \(3\)번 기둥으로 옮기려면 다음과 같은 과정을 거쳐야 한다.
- 가장 작은 원판을 \(1\)에서 \(3\)으로 옮긴다. (누적 가중치: \(1\))
- 두 번째 작은 원판을 \(1\)에서 \(2\)로 옮긴다. (누적가중치: \(2\))
- 가장 작은 원판을 \(3\)에서 \(2\)로 옮긴다. (누적 가중치: \(3\))
- 가장 큰 원판을 \(1\)에서 \(3\)으로 옮긴다. (누적 가중치: \(4\))
- 가장 작은 원판을 \(2\)에서 \(1\)로 옮긴다. (누적 가중치: \(5\))
- 두 번째 작은 원판을 \(2\)에서 \(3\)으로 옮긴다. (누적 가중치: \(6\))
- 가장 작은 원판을 \(1\)에서 \(3\)으로 옮긴다. (누적 가중치: \(7\))
이와 같은 방법으로 옮기면 \(7\)의 가중치로 \(3\)개의 원판을 \(1\)에서 \(3\)으로 옮길 수 있다. 이보다 더 적은 가중치로 모두 옮길 수 있는 방법은 없으므로 답은 \(7\)이다.
각 기둥의 관계와 출발 기둥과 도착 기둥이 차례로 주어질 때, 출발 기둥에 있는 3개의 원판을 위 규칙 1, 2를 지켜가면서 도착 기둥으로 옮기는 최소 가중치를 구하는 프로그램을 작성하시오.
*다음과 같은 확장 하노이 타워가 주어질 수도 있다.

입력 설명
첫 번째 줄에 기둥의 수 \(n(n \le 30)\)이 입력된다.
다음 줄부터 \(n\)줄에 걸쳐 각 \(n\)개의 자연수(자연수 \(< 2^{16}\))가 입력된다.
이 테이블은 각 기둥 간 이동에 대한 가중치를 나타낸다.(가중치가 \(0\)이면 이동이 불가능하다.)
마지막 줄에 시작 기둥의 번호와 도착 기둥의 번호가 공백으로 구분되어 입력된다.
다음 줄부터 \(n\)줄에 걸쳐 각 \(n\)개의 자연수(자연수 \(< 2^{16}\))가 입력된다.
이 테이블은 각 기둥 간 이동에 대한 가중치를 나타낸다.(가중치가 \(0\)이면 이동이 불가능하다.)
마지막 줄에 시작 기둥의 번호와 도착 기둥의 번호가 공백으로 구분되어 입력된다.
출력 설명
\(3\)개의 원판을 시작 기둥에서 마지막 기둥까지 모두 옮기는데 드는 최소비용을 출력한다.
입력 예시 Copy
3
0 1 1
1 0 1
1 1 0
1 3
출력 예시 Copy
7