개구리가 수직선 위의 0에서 출발해서 오른쪽(\(x\)좌표가 증가하는 방향)으로 점프들을 수행한 후 어떤 수 \(x>0\)에 도착하려 한다. 이 때, 점프 간격은 \(1\)로부터 시작해서 항상 직전 점프한 간격의 \(2\)배로 증가해야 한다. 만일 점프 간격을 \(2\)배씩 계속 증가시켜 마지막 점프에서 목표 수 \(x\)를 지나칠 것 같으면, 필요한 경우 언제든지 점프 간격을 다시 처음 상태인 간격 \(1\)로 되돌아 갈 수 있다. 이것을 재시작이라고 부른다. 예를 들어, 아래<그림1>과 같이 \(x=19\)에 도달하기 위해서 \(2\)번의 재시작을 수행해서 \((1+2+4+8)+(1+2)+(1)=19\)와 같이 \(7\)번의 점프로 도착할 수 있다.

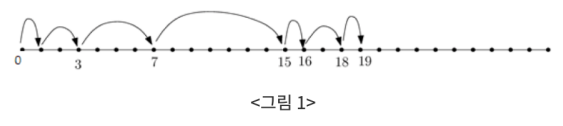
개구리가 \(0\)에서 출발해서 어떤 양의 정수 \(N\)에 도달하기 위한 점프 횟수의 최솟값을 \(J(N)\)으로 나타내고 \(N\)의 점프넘버라고 부를 것이다. 예를 들어, <그림1>을 보면 \(J(1)=1, J(3)=2, J(7)=3 J(15)=4, J(16)=5, J(19)=7\)과 같음을 알 수 있다.

여러분은 어떤 특정 구간 \([x,y]\)안의 수들의 점프 넘버들 중 최댓값을 찾아서 출력한다. 즉 아래 조건을 만족하는 \(w\)를 찾아서 출력한다.
\(w=max\{J(i) | x \le i \le y\}\)

채점 기준
제출된 프로그램은 여러 개의 테스트 케이스로 평가되며, 맞은 테스트 케이스에 대해서 해당 테스트 케이스에 배정된 점수를 받는다. 모든 테스트 케이스를 맞았을 시 100점을 받는다.

각 테스트 케이스에 대한 배점 정보와 제약 조건은 다음과 같다.
1. (10점) \(1 \le x \le y \le 20\)
2. (16점\(1 \le x \le y \le 2,000\)
3. ( 8점)\(1 \le x \le y \le 1,000,000, y-x \le 2,000\)
4. (21점)\(1 \le x \le y \le 4,000,000\)
5. (45점) 제약 조건 없음

표준 입력으로 다음 정보가 주어진다.
첫 번째 줄에는 여러분에게 주어질 구간의 개수 \(T\)가 주어진다.\((1 \le T \le 2,000)\)
이 후 \(T\)개의 줄에 대해 답을 구해야 할 구간을 나타내는 두 정수 \(x,y\)가 공백을 사이에 두고 주어진다. \(( 1\le x \le y \le 10^9)\)

표준 출력으로 \(T\)개의 줄에 각각 하나의 정수를 출력한다.
각 줄에 출력되는 정수 구간\([x,y]\)안의 수들의 점프넘버들 중 최댓값이다.
각 정수는 입력으로 주어지는 구간의 순서에 맞게 출력되어야 한다. 즉, 첫 번째 줄에 출력되는 정답은 첫 번째로 주어지는 구간에 대응되어야 한다.

	작성자	제목(댓글)
글이 없습니다.

문제 게시판

새 글 작성

2019KOI1차