문제 설명
(초1 중2)
정사각형의 종이를 중앙선을 중심으로 접는 방법은 아래 그림에서 보인 것처럼 4가지가 있다.
- D: 가로 중심선을 중심으로 반으로 접되 윗 면이 아랫 면을 덮도록 접음
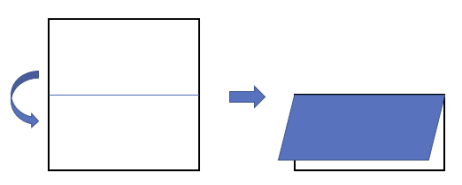
- U: 가로 중심선을 중심으로 반으로 접되 아랫 면이 윗 면을 덮도록 접음
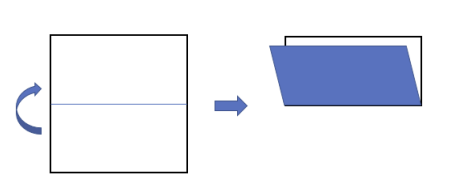
- R: 세로 중심선을 중심으로 반으로 접되 왼쪽 면이 오른쪽 면을 덮도록 접음
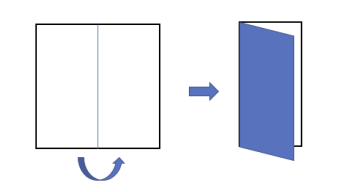
- L: 세로 중심선을 중심으로 반으로 접되 오른쪽 면이 왼쪽 면을 덮도록 접음
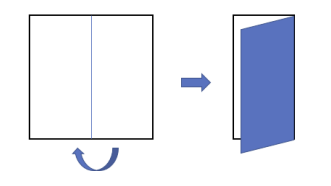
한 변의 길이가 \(2^k\)인 정사각형 종이가 있을 때, 이를 세로로 \(k\)번, 가로로 \(k\)번 접으면 (접는 순서는 상관 없음) 각 변의 길이가 \(1\)인 정사각형이 된다. 아래 그림에서 보인 것처럼 각 변의 길이가 \(1\)인 정사각형의 네 귀퉁이 중 한 군데에 구멍을 낸다. 구멍의 위치는 그림에서 보인 것처럼 숫자로 표시한다.
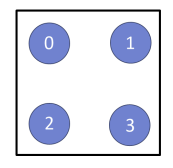
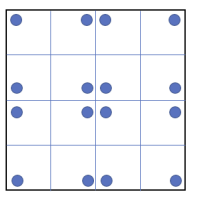
구멍을 낸 후 접은 순서의 역순으로 종이를 펼치면, 종이에 \(2^2k\)개의 구멍이 있게 된다. 예를 들어, 한 변의
길이가 \(4(= 2^2
)\)인 정사각형을
종이의 크기를 나타내는 정수 \(k\), 종이를 접는 순서를 나타내는 정보, 구멍 뚫는 위치를 나타내는 정수가 주어질 때, \(2^k \times 2^k\) 격자에 뚫린 구멍의 위치를 출력하는 프로그램을 작성하시오.
입력 설명
첫 번째 줄에 \(k\)가 주어진다.
다음 줄에는 종이 접는 방법을 나타내는 문자가 \(2k\)개 주어지는데, 각 문자는 공백으로 구분된다. 종이를 접는 방법 \(D, U, R, L\)은 각각 해당하는 대문자 알파벳으로 주어진다.
다음 줄에는 구멍 뚫는 위치를 나타내는 정수 \(h(0 \le h \le 3)\) 가 주어진다.
- \(1 \le k \le 8\)
- 반드시 가로로 \(k\)번, 세로로 \(k\)번 접는다.
- (29점) \(k = 1\)
- (34점) 종이를 접는 순서는 \(U\)와 \(R\)로만 이루어진다.
- (37점) 추가 제약 조건 없음
출력 설명
입력 예시 Copy
2
R D D R
3
출력 예시 Copy
0 1 0 1
2 3 2 3
0 1 0 1
2 3 2 3