문제 설명
가로, 세로 길이가 모두 N인 커다란 종이가 주어져 있다. 좌표 (X, Y )는 종이의 가장 왼쪽 위 점을 (0, 0)
으로 하고, (0, 0)에서 세로로 거리 X, 가로로 거리 Y 를 이동한 점을 의미한다. 따라서, 종이의 가장 오른쪽
아래 점의 좌표는 (N, N)이 된다.
C개의 점이 주어진다. 점들의 좌표는 모두 양의 정수이고, 순서대로 1부터 C까지 번호가 매겨진다. 두 개 이상의 점이 같은 좌표를 가질 수도 있다.
번호 순서대로 점들에 대해서 다음과 같은 일을 한다. 현재 종이의 세로 길이가 A, 가로 길이가 B이고, 이번 순서의 점이 (X, Y )라고 하자. 처음 시작할 때는 A와 B 모두 N과 같다.
다음 예제를 생각해보자.
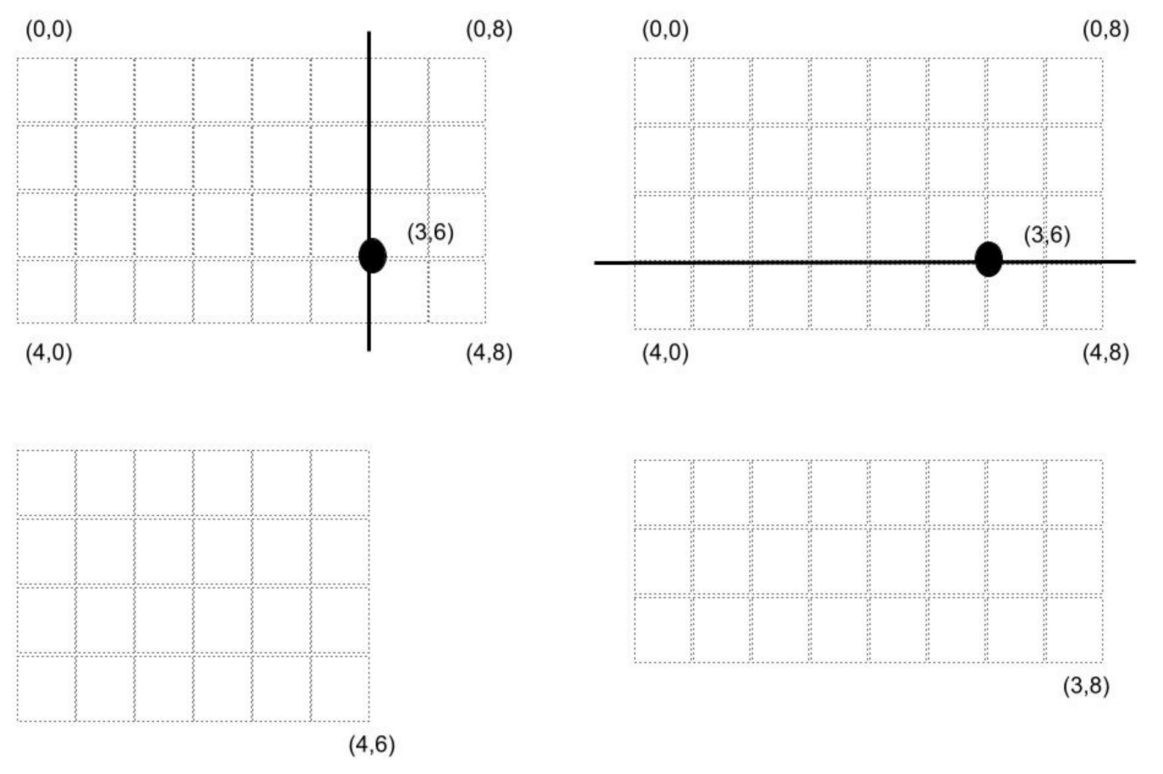
세로 길이 4, 가로 길이 8인 종이가 주어져 있는 상태에서, 점 (3, 6)을 생각해보자. 그림에서 한 칸은 면적이 1이다. 이 경우 이 점을 지나는 세로 직선으로 종이를 자르면 세로 길이 4, 가로 길이 6인 종이가 남고, 이 점을 지나는 가로 직선으로 종이를 자르면 세로 길이 3, 가로 길이 8인 종이가 남게 된다. 두 사각형은 모두 면적이 24로 같으므로 조건에 따라 가로로 잘라야 한다. 그래서, 이 예에서는 세로 길이 3, 가로 길이 8인 종이가 남는다.
위 일을 C개의 모든 점에 대해서 1번부터 C번까지 차례대로 수행했을 때, 마지막으로 남는 종이의 면적을 구하시오.
C개의 점이 주어진다. 점들의 좌표는 모두 양의 정수이고, 순서대로 1부터 C까지 번호가 매겨진다. 두 개 이상의 점이 같은 좌표를 가질 수도 있다.
번호 순서대로 점들에 대해서 다음과 같은 일을 한다. 현재 종이의 세로 길이가 A, 가로 길이가 B이고, 이번 순서의 점이 (X, Y )라고 하자. 처음 시작할 때는 A와 B 모두 N과 같다.
- 만약 점이 종이의 경계나 밖에 있다면, 즉 X ≥ A이거나, Y ≥ B라면 이 점은 무시된다.
- 만약 점이 종이 안에 있다면, 이 점을 지나는 가로 방향 직선으로 종이를 자르는 것과, 세로 방향 직 선으로 종이를 자르는 것 중 하나를 수행해야 한다. 종이를 가로로 자를 때는 위쪽을 남기고 아래쪽을 버리고, 세로로 자를 때는 왼쪽을 남기고 오른쪽을 버린다. 두 경우 중에서 남은 직사각형의 면적이 넓은 쪽을 선택해야 한다. 만약 두 경우의 남은 직사각형의 면적이 같다면, 가로로 잘라야 한다.
다음 예제를 생각해보자.

세로 길이 4, 가로 길이 8인 종이가 주어져 있는 상태에서, 점 (3, 6)을 생각해보자. 그림에서 한 칸은 면적이 1이다. 이 경우 이 점을 지나는 세로 직선으로 종이를 자르면 세로 길이 4, 가로 길이 6인 종이가 남고, 이 점을 지나는 가로 직선으로 종이를 자르면 세로 길이 3, 가로 길이 8인 종이가 남게 된다. 두 사각형은 모두 면적이 24로 같으므로 조건에 따라 가로로 잘라야 한다. 그래서, 이 예에서는 세로 길이 3, 가로 길이 8인 종이가 남는다.
위 일을 C개의 모든 점에 대해서 1번부터 C번까지 차례대로 수행했을 때, 마지막으로 남는 종이의 면적을 구하시오.
입력 설명
첫째 줄에, 두 정수 N과 C가 공백 하나씩을 사이에 두고 주어진다. 다음 C 줄에는 각 줄마다 차례대로 점
(X, Y )를 나타내는 두 정수 X와 Y 가 공백 하나씩을 사이에 두고 주어진다
- 1 ≤ N ≤ 10 000
- 1 ≤ C ≤ 10 000
- 처리할 점 (X, Y )는 모두 1 ≤ X, Y ≤ N를 만족.
- (5점) 데이터는 예제 중 하나이다.
- (15점) C = 1
- (20점) 각 점에 대해 일을 할 때, 그 점이 무시되는 점이 아니라면 항상 가로로 자르고 남은 위쪽 부분의 면적이 세로로 자르고 남은 왼쪽 부분의 면적보다 크거나 같음이 보장된다.
- (60점) 추가 제약 조건 없음.
출력 설명
첫째 줄에 마지막으로 남는 종이의 면적을 출력한다.
입력 예시 Copy
4 3
3 3
2 2
1 1
출력 예시 Copy
4