5043: 그래프 균형 맞추기
[만든사람 : ]
문제 설명
N개의 정점과 M개의 간선으로 구성된 무방향 단순 연결 그래프가 있다. 그래프의 정점들에는 1 이상 N
이하의 서로 다른 자연수 번호가 붙어 있고, 간선들에는 1 이상 M 이하의 서로 다른 자연수 번호가 붙어
있다.
j (1 ≤ j ≤ M)번 간선은 aj번 정점과 bj번 정점을 연결하며, 정수 가중치 cj가 붙어 있다.
당신은 모든 정점에 정수 가중치를 부여해야 한다. i (1 ≤ i ≤ N)번 정점에 부여할 가중치를 xi라고 하자.
정점에 가중치를 부여하는 총 비용은 각 정점의 가중치의 절댓값의 합, 즉 |x1|+|x2|+· · ·+|xN | =∑ N i=1 |xi | 과 같다.
그래프의 균형이 맞으려면, 각 간선이 연결하고 있는 두 정점의 가중치의 합이 간선의 가중치와 같아야 한다. 즉, 모든 j (1 ≤ j ≤ M)에 대해, xaj + xbj이 cj와 같아야 한다.
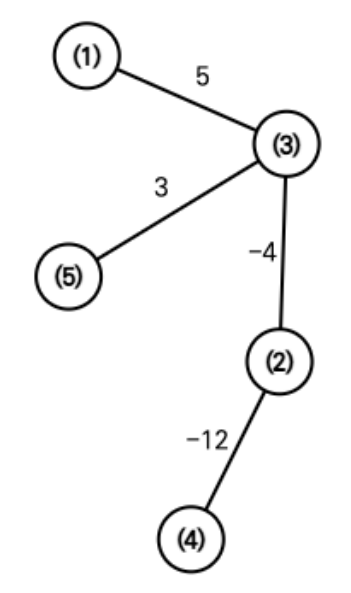
예를 들어, 아래와 같이 5개의 정점과 4개의 간선으로 이루어진 그래프를 생각하자. 그림에서 정점을 나타내는 원 안에 적힌 수는 정점의 번호이고, 간선을 나타내는 선에 적힌 수는 간선에 붙은 가중치이다.
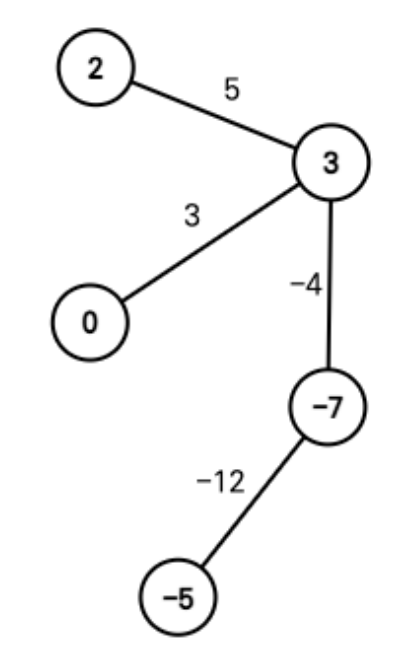
아래의 그림과 같이 각 정점에 [2, -7, 3, -5, 0]의 가중치를 부여해서, 각 간선이 연결하고 있는 두 정점의 가중치의 합이 간선의 가중치와 같게 할 수 있다. 아래 그림에서 정점을 나타내는 원 안에 적힌 수는 정점의 가중치이다.
총 비용은 |2| + | − 7| + |3| + | − 5| + |0| = 2 + 7 + 3 + 5 + 0 = 17이다. 총 비용을 17보다 작게 할 수 있는 방법은 없기 때문에, 위 방법은 총 비용을 최소화하는 방법이다.
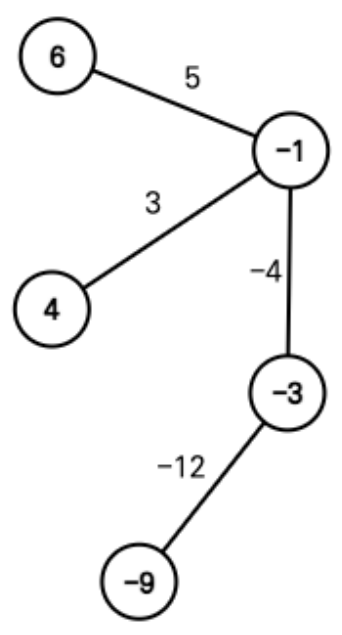
아래와 같이 각 정점에 [6, -3, -1, -9, 4]의 가중치를 부여해도 균형이 맞는 그래프가 되지만, 이 경우 총 비용은 17보다 큰 23이 되기 때문에 아래 방법은 총 비용을 최소화하는 방법이 아니다.
그래프의 균형이 맞도록 정점에 가중치를 부여하는 것이 가능한지 확인하고, 가능하다면 그 중 총 비용을 최소화하는 방법을 하나 구하는 프로그램을 작성하라.
j (1 ≤ j ≤ M)번 간선은 aj번 정점과 bj번 정점을 연결하며, 정수 가중치 cj가 붙어 있다.
당신은 모든 정점에 정수 가중치를 부여해야 한다. i (1 ≤ i ≤ N)번 정점에 부여할 가중치를 xi라고 하자.
정점에 가중치를 부여하는 총 비용은 각 정점의 가중치의 절댓값의 합, 즉 |x1|+|x2|+· · ·+|xN | =∑ N i=1 |xi | 과 같다.
그래프의 균형이 맞으려면, 각 간선이 연결하고 있는 두 정점의 가중치의 합이 간선의 가중치와 같아야 한다. 즉, 모든 j (1 ≤ j ≤ M)에 대해, xaj + xbj이 cj와 같아야 한다.
예를 들어, 아래와 같이 5개의 정점과 4개의 간선으로 이루어진 그래프를 생각하자. 그림에서 정점을 나타내는 원 안에 적힌 수는 정점의 번호이고, 간선을 나타내는 선에 적힌 수는 간선에 붙은 가중치이다.

아래의 그림과 같이 각 정점에 [2, -7, 3, -5, 0]의 가중치를 부여해서, 각 간선이 연결하고 있는 두 정점의 가중치의 합이 간선의 가중치와 같게 할 수 있다. 아래 그림에서 정점을 나타내는 원 안에 적힌 수는 정점의 가중치이다.

총 비용은 |2| + | − 7| + |3| + | − 5| + |0| = 2 + 7 + 3 + 5 + 0 = 17이다. 총 비용을 17보다 작게 할 수 있는 방법은 없기 때문에, 위 방법은 총 비용을 최소화하는 방법이다.
아래와 같이 각 정점에 [6, -3, -1, -9, 4]의 가중치를 부여해도 균형이 맞는 그래프가 되지만, 이 경우 총 비용은 17보다 큰 23이 되기 때문에 아래 방법은 총 비용을 최소화하는 방법이 아니다.

그래프의 균형이 맞도록 정점에 가중치를 부여하는 것이 가능한지 확인하고, 가능하다면 그 중 총 비용을 최소화하는 방법을 하나 구하는 프로그램을 작성하라.
참고
|x|는 x < 0이면 −x, x ≥ 0이면 x인 절댓값 기호이다입력 설명
첫째 줄에 N과 M이 순서대로 공백을 사이에 두고 주어진다.
다음 M개의 줄에 각 간선에 대한 정보가 주어진다. 이 중 j (1 ≤ j ≤ M)번째 줄에는 세 정수 aj , bj , cj가 공백 하나씩을 사이로 두고 주어진다.
다음 M개의 줄에 각 간선에 대한 정보가 주어진다. 이 중 j (1 ≤ j ≤ M)번째 줄에는 세 정수 aj , bj , cj가 공백 하나씩을 사이로 두고 주어진다.
- 주어지는 모든 수는 정수이다.
- 2 ≤ N ≤ 100 000
- 1 ≤ M ≤ 200 000
- 모든 j (1 ≤ j ≤ M)에 대해:
- 1 ≤ aj ≤ N, 1 ≤ bj ≤ N
- aj 6= bj . 즉, 서로 같은 두 정점을 연결하는 간선은 없다.
- −1 000 000 ≤ cj ≤ 1 000 000
- 모든 j, k (1 ≤ j < k ≤ M)에 대해, {aj , bj} 6= {ak, bk}. 즉, 서로 다른 두 정점 쌍 (a, b)를 잇는 간선은 많아야 한 개 존재한다.
- 그래프는 연결 그래프이다. 즉, 그래프에서 어떤 두 정점을 골라도, 간선들을 통해 두 정점을 직, 간접 적으로 잇는 경로가 존재한다.
- (6점) N = 3, M = 3이고, 세 개의 간선은 1번과 2번, 2번과 3번, 3번과 1번 정점을 각각 잇고 있다.
- (10점) N ≤ 1, 000이고, M = N − 1이고, j번 간선(1 ≤ j ≤ M)은 j번 정점과 j + 1번 정점을 잇고 있다.
- (11점) M = N − 1이고, j번째 간선(1 ≤ j ≤ M)은 j번 정점과 j + 1번 정점을 잇고 있다.
- (12점) M = N − 1이다.
- (13점) M = N이고, 모든 정점은 정확히 서로 다른 두 개의 간선과 이어져 있다.
- (29점) N ≤ 1 000이다.
- (19점) 추가 제약 조건 없음
출력 설명
만약 그래프의 균형이 맞도록 정점에 정수 가중치를 부여하는 방법이 존재한다면:
만약 그래프의 균형이 맞도록 정점에 정수 가중치를 부여하는 방법이 존재하지 않는다면:
- 첫째 줄에 Yes를 출력한다. 출력은 대소문자를 구분하지 않는다.
- 둘째 줄에 각 정점에 부여한 가중치를 나타내는 N개의 정수 x1, x2, . . ., xN을 공백 하나씩 사이에 두고 출력한다. 그래프의 균형이 맞도록 하면서 총 비용을 최소화하는 방법이 여럿 존재한다면, 그러한 방법들 가운데 어떤 것을 출력해도 된다.
만약 그래프의 균형이 맞도록 정점에 정수 가중치를 부여하는 방법이 존재하지 않는다면:
- 첫째 줄에 No를 출력한다. 출력은 대소문자를 구분하지 않는다.
입력 예시 Copy
3 3
1 2 5
2 3 4
3 1 3
출력 예시 Copy
Special Judge는 출력 예시를 확인할 수 없습니다.