문제 설명
건물 옥상에 헬리콥터가 착륙할 수 있도록 헬기 착륙장을 만들려고 한다.
헬기 착륙장은 아래와 같은 조건들을 모두 만족해야 한다.
헬기 착륙장의 크기란 동심원 중 반지름이 가장 큰 원의 반지름이며, 위의 조건에서 동심원의 개수 k와 같음을 알 수 있다.
두 헬기 착륙장이 서로 다르다는 것은, 착륙장의 크기가 서로 다르거나, 크기는 같지만 동심원에 칠해진 색의 조합이 다른 것을 의미한다.
반지름이 r인 원의 둘레를 색칠하기 위해서는 정확히 r통의 페인트가 필요하다.
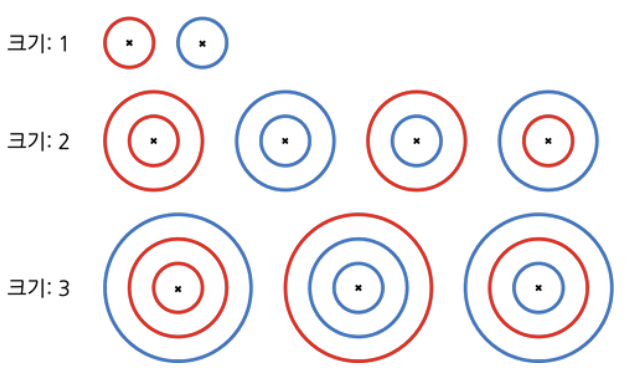
예를 들어, 빨강 페인트가 3통, 파랑 페인트가 4통 있을 때, 이 페인트를 이용하여 만들 수 있는 서로 다른 헬기 착륙장은 아래 그림에서 보인 것처럼 9가지가 있다. X 표시는 동심원의 중심을 나타낸다.
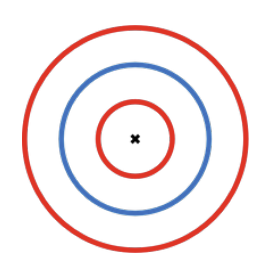
참고로, 크기가 3인 착륙장 중 아래 그림에서 보인 것처럼 그리려면 빨강 페인트 4=1+3통, 파랑 페인트 2 통이 필요한데, 주어진 빨강 페인트 3통으로는 부족하므로 이와 같은 착륙장은 만들 수 없다.
현재 당신은 빨강 페인트 a통과 파랑 페인트 b통을 갖고 있다. 이들만을 이용해 만들 수 있는 서로 다른 헬기 착륙장의 개수를 109 + 7로 나눈 나머지를 구하는 프로그램을 작성하라.
하나의 입력에서 T개의 테스트 케이스를 해결해야 한다.
헬기 착륙장은 아래와 같은 조건들을 모두 만족해야 한다.
- 헬기 착륙장은 k (k ≥ 1)개의 동심원들로 구성된다.
- 헬기 착륙장을 구성하는 각 원의 반지름은 1, 2, . . ., k (1 이상 k 이하의 서로 다른 자연수)이다.
- 각 원의 둘레는 한 가지 색의 페인트로 색칠되어야 한다.
헬기 착륙장의 크기란 동심원 중 반지름이 가장 큰 원의 반지름이며, 위의 조건에서 동심원의 개수 k와 같음을 알 수 있다.
두 헬기 착륙장이 서로 다르다는 것은, 착륙장의 크기가 서로 다르거나, 크기는 같지만 동심원에 칠해진 색의 조합이 다른 것을 의미한다.
반지름이 r인 원의 둘레를 색칠하기 위해서는 정확히 r통의 페인트가 필요하다.
예를 들어, 빨강 페인트가 3통, 파랑 페인트가 4통 있을 때, 이 페인트를 이용하여 만들 수 있는 서로 다른 헬기 착륙장은 아래 그림에서 보인 것처럼 9가지가 있다. X 표시는 동심원의 중심을 나타낸다.

참고로, 크기가 3인 착륙장 중 아래 그림에서 보인 것처럼 그리려면 빨강 페인트 4=1+3통, 파랑 페인트 2 통이 필요한데, 주어진 빨강 페인트 3통으로는 부족하므로 이와 같은 착륙장은 만들 수 없다.

현재 당신은 빨강 페인트 a통과 파랑 페인트 b통을 갖고 있다. 이들만을 이용해 만들 수 있는 서로 다른 헬기 착륙장의 개수를 109 + 7로 나눈 나머지를 구하는 프로그램을 작성하라.
하나의 입력에서 T개의 테스트 케이스를 해결해야 한다.
입력 설명
첫 번째 줄에는 테스트 케이스의 수 T 가 주어진다.
다음 T개의 줄에는 테스트 케이스들이 한 줄에 하나씩 주어진다. 각 줄에는 두 정수 a와 b가 공백 하나를 사이로 두고 주어진다.
다음 T개의 줄에는 테스트 케이스들이 한 줄에 하나씩 주어진다. 각 줄에는 두 정수 a와 b가 공백 하나를 사이로 두고 주어진다.
- 주어지는 모든 수는 정수이다.
- 1 ≤ T ≤ 10 000
- 1 ≤ a, b ≤ 50 000
- (3점) T = 1. a, b ≤ 6.
- (17점) T = 1. a, b ≤ 100.
- (21점) T = 1. a, b ≤ 1 000.
- (23점) T = 1. a, b ≤ 5 000.
- (26점) T = 1.
- (10점) 추가 제약 조건 없음.
출력 설명
각 테스트 케이스에 대해, 한 줄에 하나씩, 빨강 페인트 a통과 파랑 페인트 b통만을 이용해 만들 수 있는
서로 다른 헬기 착륙장의 수를 109 + 7로 나눈 나머지를 출력한다.
입력 예시 Copy
3
3 4
10 5
7 12
출력 예시 Copy
9
25
40