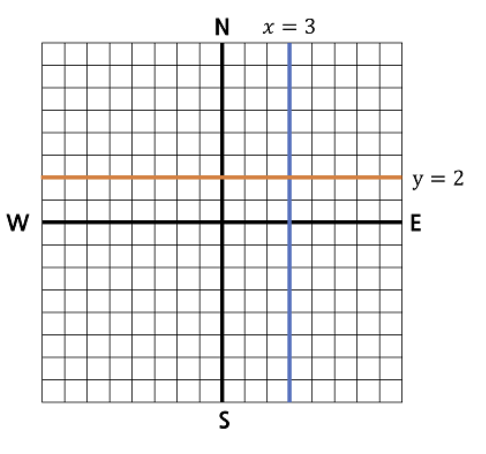
KOI시는 너무나 커다라서, 이동하려면 시간이 오래 걸린다. 그래서 KOI시는 도시를 관통하는 아주 긴 도로를 건설하였다. 도로는 남북 방향 또는 동서 방향으로 무한히 뻗어 나간다. 남북 방향의 도로는 총 \(N\)개 이고, 동서 방향의 도로는 총 \(M\)개이다. 도로의 폭은 충분히 좁아 무시할 수 있다. KOI시의 시청을 원점으로 삼아 도시를 좌표평면 위에 그리면 남북 방향 도로는 \(x = a_i (1 \le i \le N)\)인 직선으로, 동서 방향 도로는 \(y = b_j (1 \le j \le M)\) 인 직선으로 표현할 수 있다. 아래는 \(x = 3\)인 도로와 \(y = 2\)인 도로의 예이다. 그림에서는 도로가 유한하지만, 실제로는 무한히 뻗어 나감에 주의하라.

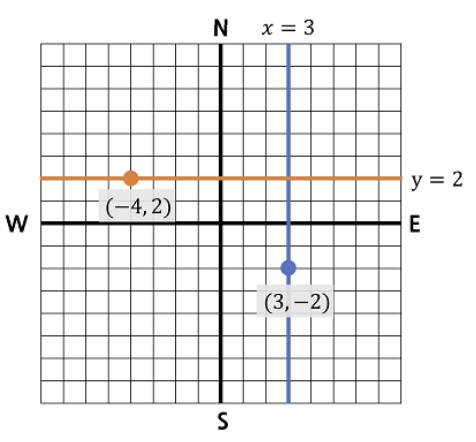
\(N + M\)개의 도로 중 \(K\)개의 도로에는 과속을 단속하기 위해 담당 경찰을 정확히 한 명씩 배치하였다. \(k (1 \le k \le K)\)번째 경찰의 위치는 \((p_k, q_k)\)이다. 담당 경찰은 반드시 자신이 담당하는 도로 위에 위치한다. 아래는 \(x = 3\) 도로의 (3, −2) 지점에 경찰이 배치되고, \(y = 2\) 도로의 (−4, 2) 지점에 경찰이 배치된 예이다. 경찰이 배치되지 않은 도로가 있을 수 있고, 어떤 도로에 경찰이 배치되었다면 반드시 한 명이라는 것에 주의하라.

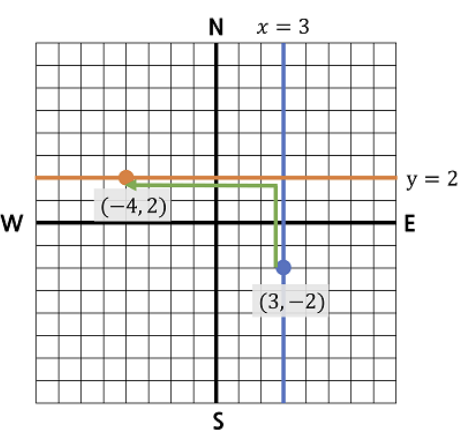
경찰은 도로 위를 이동할 수 있다. 경찰은 도로 위에서만 움직인다. 만약 두 도로가 교차한다면, 경찰은 그 지점에서 다른 도로로 옮겨갈 수 있다. 옮겨가는 데 드는 거리는 무시한다. 아래는 경찰이 다른 경찰의 위치로 움직이는 예시로, 이 경우에 경찰은 교점 (3, 2) 위에서 \(x = 3\) 직선을 나와 \(y = 2\)로 옮겨가게 된다. 총 11만큼 이동하였다.

경찰들은 만약의 사태에 다른 경찰과 빠르게 만날 수 있어야 한다. 당신은 각 경찰이 다른 경찰과 만나는 모든 경우에 대해 경찰의 최소 이동 거리를 구하여 그 합을 계산해야 한다. 아래 예시를 보자.

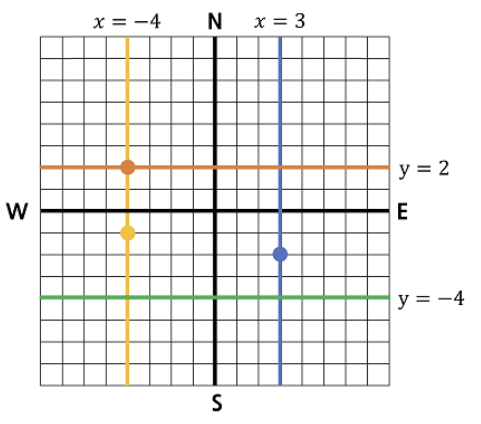
이 경우에는 총 3가지 경우가 있다.

• \(y = 2\) 도로의 담당 경찰과 \(x = −4\) 도로의 담당 경찰이 만난다. 이 경우 두 경찰은 최소 3만큼을 이동해야 만날 수 있다. 
• \(y = 2\) 도로의 담당 경찰과 \(x = 3\) 도로의 담당 경찰이 만난다. 이 경우 두 경찰은 최소 11만큼을 이동해야 만날 수 있다. 
• \(x = −4\) 도로의 담당 경찰과 \(x = 3\) 도로의 담당 경찰이 만난다. 이 경우 두 경찰은 최소 12만큼을 이동해야 만날 수 있다.

따라서 총합은 26이 된다. \(x\)좌표가 −4인 경찰이 두 명 존재하지만, 경찰 (−4, 2)는 도로 \(y = 2\)에 있고 경찰 (−4, −1)은 도로 \(x = −4\) 위에 있으므로 유효한 입력임에 주의하라.

KOI시의 도로와 경찰들의 위치가 주어질 때, 위와 같이 두 경찰이 만나는 모든 경우에 대해 최소 이동 거리의 합을 출력하는 프로그램을 작성하라.

첫 번째 줄에 정수 \(N, M, K\)가 공백 하나씩을 사이에 두고 주어진다.

두 번째 줄에 \(N\)개의 정수 \(a_1, a_2, · · ·, a_N\)이 공백 하나씩을 사이에 두고 주어진다.

세 번째 줄에 \(M\)개의 정수 \(b_1, b_2, · · ·, b_M\)이 공백 하나씩을 사이에 두고 주어진다.

그 다음 \(K\)개의 줄에는 경찰들의 위치가 주어지는데, 이 중 \(k (1 \le k \le K)\)번째 줄에는 두 정수 \(p_k\)와 \(q_k\)가 공백 하나를 사이에 두고 주어진다. 

• 주어지는 모든 수는 정수이다. 
• \(1 \le N \le 100 000 \)
• \(1 \le M \le 100 000 \)
• \(2 \le K \le N + M \)
• \(100 000 \le a_i \le 100 000 (1 \le i \le N) \)
• \(100 000 \le b_j \le 100 000 (1 \le j \le M)\)
• \(100 000 \le p_k, q_k \le 100 000 (1 \le k \le K) \)
• 같은 위치에 도로나 경찰이 여럿 존재하지 않는다. 즉:
• \( – a_1, a_2, · · ·, a_N\)는 서로 다르다.
• \( – b_1, b_2, · · ·, b_M\)는 서로 다르다.
• \( – (p_1, q_1), (p_2, q_2), · · ·, (p_K, q_K)\)는 서로 다르다.
• 한 도로 위에는 한 명 이하의 경찰만 위치한다.

1. (14점) \(M = 1. \)
2. (11점) 모든 경찰은 두 도로가 교차하는 지점에만 배치된다. 
3. (20점) \(1 \le N, M \le 20. \)
4. (25점) \(1 \le N, M \le 1 000. \)
5. (30점) 추가 제약 조건 없음.