\(N\)개의 카드가 놓여있다. 편의상 가장 왼쪽에 있는 카드를 1번 카드, 그 다음에 있는 카드를 2번 카드 . . . 가장 오른쪽에 있는 카드가 \(N\)번 카드라고 하자.

  \(N\)개의 카드에는 각각 정수가 하나씩 적혀있다. \(i\)번 카드에 적혀있는 수를 \(x_i\)라고 하자. 

  \(N\)개의 카드 중 일부에 적혀있는 수들을 적절히 바꾸어서, 왼쪽에서 오른쪽으로 갈수록 카드에 적혀있는 수들이 일정하게 증가하거나, 감소하거나, 또는 모든 수들이 같도록 하고 싶다. 

카드에 적혀있는 수들을 바꿀 때는 정수 값으로만 바꿀 수 있으며, 바꾸는 횟수를 최소화해야 한다. 예를 들어, 아래의 그림과 같이 카드들이 주어졌다고 하자.

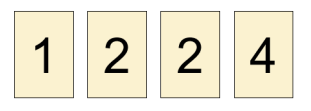
이 경우 3번 카드에 적혀있는 수를 3으로 바꾸면 아래와 같이 1씩 증가하도록 할 수 있고, 적혀있는 수를 바꾼 카드의 수는 1개이다. 

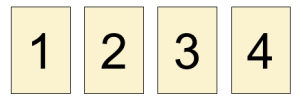
다음과 같이 모든 카드에 적혀있는 수를 2가 되도록 할 수도 있다. 이때, 적혀있는 수를 바꾼 카드의 수는 2개이다.

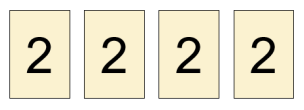
가장 왼쪽에 있는 카드부터 가장 오른쪽에 있는 카드까지 각 카드에 적혀있는 수들이 순서대로 주어질 때, 조건을 만족하도록 하려면 바꿔야 할 카드 수의 최솟값을 구하여라.

첫 번째 줄에 카드의 수 \(N\)이 주어진다. 

두 번째 줄에는 각 카드에 적힌 수 \(x_i\)가 공백을 사이에 두고 순서대로 주어진다. 

• \(2 \le N \le 500 \)
• 모든 \(1 \le i \le N\) 에 대해 \(-1 000 000 \le x_i \le 1 000 000\)

1. (3점) \(N \le 3. \)
2. (10점) 답이 2 이하이다. 
3. (20점) 최소한의 카드들만 바꿔서 조건을 만족하게 했을 때, 인접한 카드에 적힌 수의 차가 100 이하인 경우가 존재함이 보장된다. 
4. (67점) 추가 제약 조건 없음.