문제 설명
1부터 \(N\)까지 \(N\) 개의 정점으로 이루어진 트리가 있다. \(i\) 번째 간선은 서로 다른 두 정점 \(A_i , B_i\)를 잇는다. \((1 \le i \le N − 1)\)
\(N\) 개의 정점 중 몇 개를 골라, 그 고른 정점들을 \(S = \{s_1, s_2, · · · , s_K\}\)라고 하자. 또한, \(s_i = v\)를 만족하는 \(i (1 \le i \le K)\)가 존재할 때, 정점 \(v\)가 \(S\)에 속한다고 부르자.
\(S\)에 속하는 서로 다른 두 정점 \(u, v\)에 대하여, \(S\)에 속하는 정점만을 이용하여 트리 위에서 \(u, v\) 사이를 오갈 수 있다면, “\(u\)와 \(v\)는 \(S\) 위에서 연결되어 있다”고 하자.
예를 들어, 아래와 같은 트리를 생각하자. \((N = 7) \)
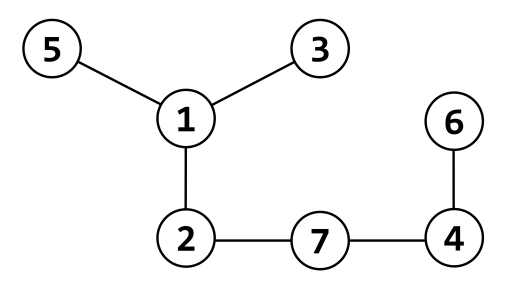
만일, \(K = 6, S = \{1, 2, 3, 4, 5, 6\}\)라면, “1과 2”, “3과 5”, “4와 6”은 각각 서로 \(S\) 위에서 연결되어 있다. 그러나, “1과 6”, “2와 7”은 각각 서로 \(S\) 위에서 연결되어 있지 않다.
다음 조건을 모두 만족하는 정점쌍 \((u, v)\)의 개수를 \(S\)의 연결 강도라고 하자.
- \(u\)와 \(v\)는 서로 다른 두 정점.
- \(1 \le u < v \le N. \)
- \(u\)와 \(v\)는 \(S\) 위에서 연결되어 있다.
고른 정점들 \(S\)가 주어질 때, \(S\)의 연결 강도를 계산하는 프로그램을 작성하라. 여러분은 이러한 질의 \(Q\) 개에 대하여 모두 답해야 한다.
입력 설명
첫 번째 줄에 정수 \(N\)이 주어진다.
다음 \((N − 1)\) 개의 줄에 각 간선에 대한 정보가 주어진다. 이 중 \(i (1 \le i \le N − 1)\) 번째 줄에는 두 정수 \(A_i , B_i\)가 주어진다.
다음 줄에 정수 \(Q\)가 주어진다.
다음 \(Q\) 개의 줄에 각 질의에 대한 정보가 주어진다. 이 중 \(i (1 \le i \le Q)\) 번째 줄은 \(i\) 번째 질의를 나타내며, 정수 \(K\)와 \(K\) 개의 정수 \(s_1, · · · , s_K\)가 차례대로 주어진다.
- \(2 \le N \le 250 000\)
- \(1 \le Q \le 100 000\)
- 모든 \(i (1 \le i \le N − 1)\)에 대해, \(1 \le A_i \le N.\)
- 모든 \(i (1 \le i \le N − 1)\)에 대해, \(1 \le B_i \le N.\)
- 모든 \(i (1 \le i \le N − 1)\)에 대해, \(A_i \ne B_i\) .
- 주어지는 그래프는 트리이다.
- 모든 질의에 대해, \(1 \le K \le N.\)
- 각 질의에서, 모든 \(i (1 \le i \le K)\)에 대해, \(1 \le s_i \le N.\)
- 각 질의에서, 고른 \(K\)개의 정점 \(s_1, · · · , s_K\)는 서로 다르다.
- \(Q\) 개의 질의에서 주어지는 \(K\)들의 합은 1 000 000 이하이다.
- (3점) \(N = 3. \)
- (10점) \(N \le 50, Q \le 50. \)
- (11점) \(N \le 2 500, Q \le 2 500. \)
- (13점) 각 질의에서, \(K = 3. \)
- (63점) 추가 제약 조건 없음.
출력 설명
입력 예시 Copy
7
1 2
1 3
1 5
2 7
4 6
4 7
6
1 1
2 1 2
4 1 2 3 4
5 1 2 4 6 7
6 1 2 3 4 5 6
7 1 2 3 4 5 6 7
출력 예시 Copy
0
1
3
10
7
21