좌표평면에 빨간색 점 \(N\)개와 파란색 점 \(M\)개가 있다. 또한, 자연수 \(W, H\)가 주어진다.

  \(i\)번째 \((1 \le i \le N)\) 빨간색 점의 좌표는 \((rx_i , ry_i)\)이고, \(j\)번째 \((1 \le j \le M)\) 파란색 점의 좌표는 \((bx_j , by_j )\) 이다. 모든 점들의 좌표는 서로 다르다.

  가로 \(W\), 세로 \(H\)인 직사각형을 변이 좌표축에 평행하고 꼭짓점이 정수 좌표에 놓이도록 할 것이다. 이 때 직사각형이 포함하는 빨간색 점과 파란색 점의 개수의 차가 가장 크게 만들고 싶다.

  직사각형이 점을 포함한다는 것은, 직사각형의 왼쪽 아래 꼭짓점 좌표가 \((a, b)\)이고 점의 좌표가 \((x, y)\)일 때 \(a \le x \le a + W, b \le y \le b + H\)를 만족한다는 것이다.

  개수의 차의 최댓값을 구하고, 그 답에 해당하는 직사각형의 위치를 찾아라.

  아래 예는 평면에 빨간색 점 3개와 파란색 점 4개가 있는 상황을 보여 준다. 원래 각 점에는 크기가 없지만 설명의 편의상 빨간색 점은 동그라미, 파란색 점은 세모로 표시하였다. 

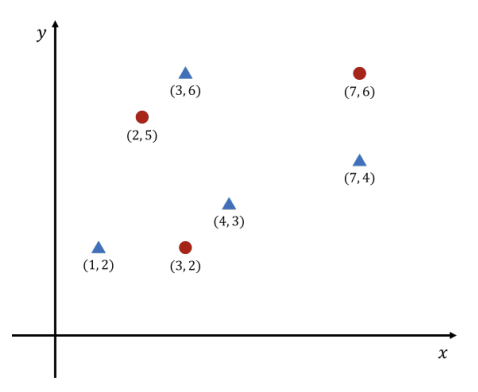
  \(W = 5, H = 3\)으로 주어졌다고 하자. 그 경우 아래와 같이 직사각형의 왼쪽 아래 꼭짓점을 (3, 3)에 놓으면 포함하는 빨간색 점이 1개, 파란색 점이 3개가 되어 개수의 차가 2가 된다. 직사각형을 어디에 놓더라도 개수의 차를 3 이상으로 만들 수는 없기 때문에 답은 2가 된다. 

  첫 번째 줄에 빨간색 점의 개수 \(N\)과 파란색 점의 개수 \(M\), 직사각형의 가로 및 세로 길이 \(W\)와 \(H\)가 각각 주어진다.

  그 다음 줄부터 \(N\)개의 줄에 걸쳐 각 빨간색 점의 \(x, y\)좌표 \(rx_i , ry_i\)가 주어진다.

  그 다음 줄부터 \(M\)개의 줄에 걸쳐 각 파란색 점의 \(x, y\)좌표 \(bx_j , by_j\)가 주어진다.
제약조건

• \(1 \le N, M \le 100 000 \)
• \(1 \le W, H \le 10^9 \)
• \(1 \le rx_i , ry_i \le 10^9 (1 \le i \le N) \)
• \(1 \le bx_j , by_j \le 10^9 (1 \le j \le M)\)

• (5점) \(1 \le N, M, W, H, rx_i , ry_i , bx_j , by_j \le 50.\)
• (11점) \(1 \le N, M, W, H, rx_i , ry_i , bx_j , by_j \le 1 000. \)
• (15점) \(1 \le N, M \le 100. \)
• (9점) \(1 \le N, M \le 1 000. \)
• (60점) 추가 제약 조건 없음.

첫 번째 줄에 빨간색 점과 파란색 점의 개수의 차의 최댓값을 출력한다.

두 번째 줄에 직사각형의 왼쪽 아래 꼭짓점의 \(x, y\)좌표를 출력한다. 답이 여러 개라면 아무 것이나 출력한다.