문제 설명
KOI 도시는 \(N\) 개의 교차로와 \(N − 1\) 개의 양방향 도로로 이루어져 있으며, 임의의 서로 다른 두 교차로를 도로만을 사용하여 오갈 수 있다. 즉, 도시의 도로망은 트리 구조를 이룬다. 도로는 2차원 평면 상에 있으며, 두 도로가 끝점을 제외한 위치에서 교차하지 않는다. 각 도로에는 0 이상의 정수 가중치가 존재하며, 이 가중치는 각 도로를 이용하는 데 걸리는 시간을 의미한다.
KOI 도시는 몇십년 전까지만 하여도 작은 마을이었지만, 사람이 유입되고 크기가 커지면서 급격히 팽창 하기 시작하였다. 급격한 팽창 과정에서 시장은 행정 편의를 위해 교차로에 1 이상 \(N\) 이하의 번호를 매겼다. 이 때 번호 시스템은 다음과 같은 성질을 만족한다.
- 1번 교차로는 도시의 중심으로, 2개 이상의 도로와 인접함이 보장된다.
- 교차로에 매겨진 번호는 1번 교차로를 루트로 한 트리의 전위 순회 순서 (Preorder) 중 하나이다.
- 모든 교차로에 대해서, 인접한 (도로로 직접 연결된) 교차로 중 가장 번호가 작은 교차로를 생각해 보자. 이 교차로를 기준으로 시계 반대 방향으로 인접한 교차로의 번호를 나열했을 때, 번호는 증가한다.
KOI 도시에 많은 사람들이 유입되면서, 교통 체증 문제가 심화되었다. 시장은 이를 해결하기 위해 교통 인프라가 가장 빈약한 도시들을 외곽 순환 도로로 이었다. KOI 도시에 있는 모든 교차로 중, 단 1개의 도로 와 인접한 교차로들의 번호를 증가하는 순서대로 나열한 리스트를 \(\{v_1, v_2, . . . , v_k\}\) 라고 하자. 시장은, 모든 \(1 \le i \le k\) 에 대해서, \(v_i\) 번 교차로와 \(v_{(i mod k)+1}\) 번 교차로를 잇는 양방향 도로를 건설하였다. 각 도로의 가중치는 0 이상의 정수 \(w_i\) 이며, 이는 입력으로 주어진다. 번호 시스템의 특성상, 두 도로가 끝점을 제외한 위치에서 교차하지 않게끔 외곽 순환 도로를 이을 수 있음을 관찰하면 좋다.
당신은 KOI 도시의 내비게이션 시스템을 구축하려고 한다. 내비게이션 시스템은, \(Q\) 개의 질의 \(u, v\) 가 주어졌을 때, \(u\) 번 교차로에서 \(v\) 번 교차로로 이동하는 데 걸리는 최소 시간을 출력해야 한다. \(u\) 번 교차로에서 \(v\) 번 교차로로 이동하는 데 걸리는 최소 시간은, \(u\) 번 교차로와 \(v\) 번 교차로를 잇는 경로들 중 가중치 합의 최솟값과 같다.
도로망 구조가 주어졌을 때, \(Q\) 개의 질의를 효율적으로 응답하는 프로그램을 작성하여라.
입력 설명
첫 번째 줄에 KOI 도시의 교차로 수 \(N\) 이 주어진다.
이후 \(N − 1\) 개의 줄이 주어진다. 이 중 \(i\) 번째 줄에는, 두 정수 \(p_i , c_i\) 가 공백으로 구분되어 주어진다. 이는, 교차로 \(p_i\) 와 교차로 \(i + 1\) 를 잇는 가중치 \(c_i\) 의 양방향 도로가 존재함을 뜻한다.
외곽 순환 도로 건설 전 1개의 도로와 인접한 교차로의 수를 \(k\) 라고 하고, 1개의 도로와 인접한 교차로들의 번호를 증가하는 순서대로 나열한 리스트를 \({v_1, v_2, . . . , v_k}\) 라고 하자. 다음 줄에, \(k\) 개의 정수 \(w_1, w_2, . . . , w_k\) 가 공백으로 구분되어 주어진다. 이는, 외곽 순환 도로의 \(v_i\) 번 교차로와 \(v_{i mod k+1}\) 번 교차로를 잇는 양방향 도로의 가중치가 \(w_i\) 임을 뜻한다.
다음 줄에 질의의 수 \(Q\) 가 주어진다.
이후 \(Q\) 개의 줄에 최소 시간을 알고 싶은 두 교차로의 번호 \(u, v\) 가 주어진다.
- \(4 \le N \le 100 000\)
- \(1 \le p_i \le i\)
- \(0 ≤ c_i , w_i ≤ 10^{12}\)
- \(1 \le Q \le 250 000\)
- \(1 \le u, v \le N, u \ne v \)
- (6점) 모든 쿼리에 대해 \(u = 1. \)
- (8점) 모든 \(1 \le i \le N − 1\) 에 대해 \(p_i = 1. \)
- (5점) 모든 \(1 \le i \le N − 1\) 에 대해 \(c_i \le 10^6\) , 모든 \(1 \le i \le k\) 에 대해 \(w_i = 10^{12}\) .
- (15점) 모든 \(1 \le i \le k\) 에 대해 \(w_i = 0\).
- (57점) 4개 이상의 도로와 인접한 교차로가 존재하지 않음.
- (9점) 추가 제약 조건 없음.
출력 설명
입력 예시 Copy
4
1 9
1 8
1 0
9 9 9
6
1 2
1 3
1 4
2 3
2 4
3 4
출력 예시 Copy
9
8
0
9
9
8
도움
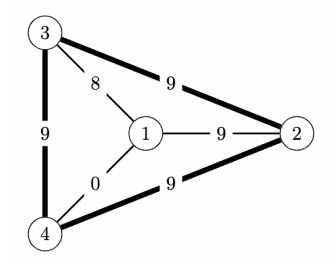
위 지도는 샘플입력에 대응된다. 샘플입력은 부분문제 2, 5, 6의 조건을 만족한다.