문제 설명
여러분은 2차원 지도에서 자동차를 조종하며 아이템을 모으는 게임을 제작하고 있다.
지도에는 아이템을 얻을 수 있는 \(N\)개의 상자가 있다. \(i\)번째 상자의 위치는 \((x_i , y_i)\)이고, 자동차가 이 위치를 지날 때마다 \(w_i\)개의 아이템을 얻을 수 있다.
자동차는 \(x\)축 또는 \(y\)축에 평행한 방향으로 이동한다. 자동차의 이동은 두 정수 \(d\)와 \(v\)로 표현할 수 있다. \(d = 0\)이면 \(x\)좌표가 증가하는 방향으로 \(v\)만큼, \(d = 1\)이면 \(y\)좌표가 증가하는 방향으로 \(v\)만큼, \(d = 2\)이면 \(x\) 좌표가 감소하는 방향으로 \(v\)만큼, \(d = 3\)이면 \(y\)좌표가 감소하는 방향으로 \(v\)만큼 이동한다.
이때 이동이 시작되는 위치에 있는 상자의 아이템은 얻을 수 없다. 즉, \((s_x, s_y)\)에서 \((e_x, e_y)\)로 이동하는 경우, \((s_x, s_y)\)에 있는 상자의 아이템은 얻을 수 없고, \((e_x, e_y)\)에 있는 상자의 아이템은 얻을 수 있다.
자동차는 (1, 1)에서 시작해 총 \(Q\)번 이동한다. 자동차의 이동 방향과 거리가 주어지면, \(Q\)번의 이동에서 얻게 되는 아이템의 총 개수를 구하시오.
입력 설명
첫 번째 줄에 상자의 개수 \(N\)과 이동 횟수 \(Q\)가 공백으로 구분되어 주어진다.
이후 \(N\)개의 줄이 주어진다. 이 중 \(i\)번째 줄에는 세 정수 \(x_i, y_i, w_i\)가 공백으로 구분되어 주어진다. 이는 \(i\)번째 상자가 \((x_i, y_i)\)에 있으며, 이 위치를 지날 때마다 \(w_i\)개의 아이템을 얻게 됨을 의미한다.
이후 \(Q\)개의 줄이 주어진다. 이 중 \(j\)번째 줄에는 두 정수 \(d_j , v_j\)가 공백으로 구분되어 주어진다. 이는 자동차가 \(d_j\)방향으로 \(v_j\)만큼 이동함을 의미한다
제약 조건
- \(1 \le N \le 200 000\)
- \(\le Q \le 200 000\)
- \(1 \le x_i \le 200 000\)
- \(1 \le y_i \le 200 000\)
- \(1 \le w_i \le 200 000\)
- \(0 \le d_j \le 3\)
- \(1 \le v_j \le 200 000\)
- 상자의 위치는 서로 다르다.
- 매 순간 자동차의 \(x, y\)좌표는 1 이상 200 000 이하이다.
- 주어지는 수는 모두 정수이다.
부분문제
- (9점) \(N \le 2 000, Q \le 2 000, x_i \le 1 000, y_i \le 1 000, w_i \le 10\), 매 순간 자동차의 \(x, y\)좌표는 1 000 이하이다.
- (17점) \(N \le 2 000, Q \le 2 000, w_i \le 10\)
- (15점) 모든 상자의 \(x\)좌표가 서로 다르고, \(y\)좌표가 서로 다르다.
- (37점) \(w_i = 1\)
- (22점) 추가 제약 조건 없음.
출력 설명
입력 예시 Copy
4 6
5 5 3
5 8 5
3 5 2
1 5 1
0 4
1 9
3 5
2 3
2 1
0 5
출력 예시 Copy
24
도움
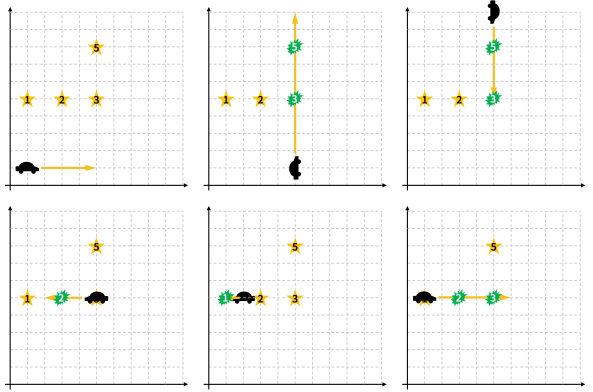
이동할 때마다 초록색으로 표시된 아이템을 얻는다.