첫 번째 줄에는 1개의 수를, 두 번째 줄에는 2개의 수를, . . . ,\( N\)번째 줄에는 \(N\)개의 수를 아래 그림과 같이 배치한 정삼각형 \(A, B\)가 주어진다. 각 위치에 있는 수는 0 또는 1이다.

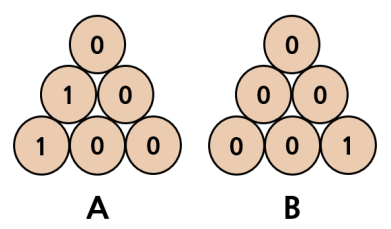
당신은 정삼각형을 시계방향 또는 반시계 방향으로 \(120^{\circ}\) 회전시키거나 좌우로 대칭시킬 수 있다. 예를 들어, 위 그림의 정삼각형 \(A\)를 회전시켜서 얻을 수 있는 정삼각형들은 다음과 같다.

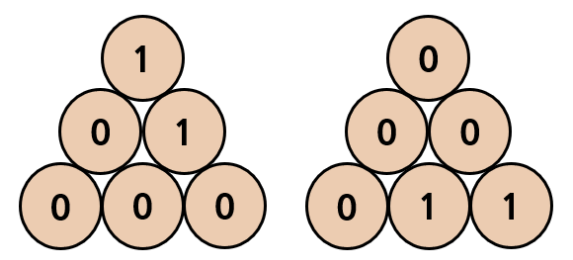
\(A\)를 대칭시켜서 얻을 수 있는 정삼각형은 다음과 같다. 

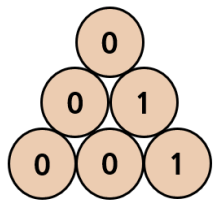
두 정삼각형의 차이는 두 정삼각형을 겹쳤을 때 값이 다른 위치의 개수이다. 

예를 들어, 정삼각형 \(A\)와 \(B\)를 겹쳐보면, 두 번째 줄에서 가장 왼쪽, 세 번째 줄에서 가장 왼쪽과 오른쪽에 있는 수들이 다르므로, \(A\)와 \(B\)의 차이는 3이 된다.

반면에,\(A\)를 반시계 방향으로 \(120^{\circ}\) 회전시킨 삼각형(두 번째 그림에서 오른쪽 삼각형)과 \(B\)를 겹쳐보면 세 번째 줄에서 왼쪽에서 두 번째에 있는 수들만 다르므로, 이때 정삼각형의 차이는 1이 된다.

정삼각형\( A\)와 \(B\)가 주어진다. 당신은 \(A\)를 원하는 만큼 회전시키고 대칭시킬 수 있다. 물론 \(A\)를 회전시키 거나 대칭시키지 않아도 된다. 또한, 회전시키거나 대칭시킬 수 있는 횟수에는 제한이 없다.

위와 같이 \(A\)를 회전시키거나 대칭시켜 \(B\)와 차이가 최소로 나게 하자. 이때 차이가 얼마인지 구하시오. 

첫 번째 줄에 \(A, B\)의 크기 \(N\)이 주어진다.

두 번째 줄부터 \(N + 1\)번째 줄까지, \(A\)의 각 위치에 있는 수들이 주어진다.

\(i + 1(1 \le i \le N)\)번째 줄에는 \(A\)의 \(i\)번째 줄에 있는 \(i\)개의 정수가 왼쪽부터 공백을 사이에 두고 순서대로 주어진다.

\(N + 2\)번째 줄부터 \(2N + 1\)번째 줄까지, \(B\)의 각 위치에 있는 수들이 주어진다.

\(i + N + 1(1 \le i \le N)\)번째 줄에는 \(B\)의 \(i\)번째 줄에 있는 \(i\)개의 정수가 왼쪽부터 공백을 사이에 두고 순서대로 주어진다.

제약 조건

• 주어지는 모든 수는 정수이다.
• \(1 \le N \le 10\)
• \(A, B\)의 각 위치에 있는 수는 0또는 1이다.

부분문제

1. (5점) \(A\)에 배치되어 있는 모든 수들이 같다. 다시 말해 \(A\)에는 모두 0이 써 있거나, 모두 1이 써 있다.
2. (10점) \(N \le 2\)
3. (40점) \(A\)를 회전시킨 경우만 고려해도 정답을 찾을 수 있다.
4. (45점) 추가 제한 없음.