한국이와 정올이는 격자 모양의 보드에서 한국이부터 차례로 번갈아가며 말을 움직이는 게임을 한다. 자신의 차례를 건너뛸 수 없다. 

보드는 \(N\)개의 행과 \(M\)개의 열로 이루어져 있으며, 보드의 일부 칸은 막혀 있다. 막혀 있는 칸으로는 말을 움직일 수 없다. 편의상 보드의 (위에서 부터) \(i\)번째 행과 (왼쪽에서 부터) \(j\)번째 열이 만나는 지점에 위치한 칸을 \((i, j)\)로 표기하자.

 말은 한 번에 아래로 한 칸, 오른쪽으로 한 칸 또는 오른쪽 아래 대각선 방향으로 \(1, 2, · · · , K\)칸 움직일 수 있다. (단, 보드의 밖이나 막혀 있는 칸으로 움직일 수는 없으며, \(K = 0\)인 경우에는 대각선 방향으로 움직일 수 없다.)

 말을 움직이는 규칙과 관련한 몇 가지 예시를 살펴보자. 

 예를 들어, \(N = 6, M = 8, K = 3\)이고 막혀 있는 칸이 없는 보드를 생각하자. (2, 3)에 놓인 말이 움직일 수 있는 칸은 총 5개로 다음 그림에 \(\bigcirc\) 표시된 것과 같다.

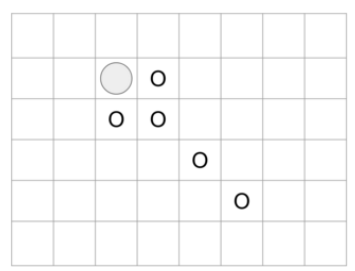
위의 상황에서 (2, 4)와 (4, 5)가 막혀 있다고 가정하자. 이 경우에 (2, 3)에 놓인 말이 움직일 수 있는 칸은 총 3개로 다음 그림에 \(\bigcirc\)  표시된 것과 같다.

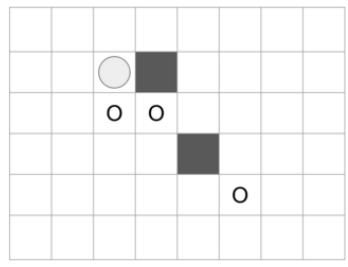
다음 그림과 같이 \(N = 6, M = 8, K = 3\)이고 막혀 있는 칸이 없는 보드를 생각하자. 이 보드에서 (5, 7)에 놓인 말이 움직일 수 있는 칸은 총 3개로 다음 그림에 \(\bigcirc\) 표시된 것과 같다. 

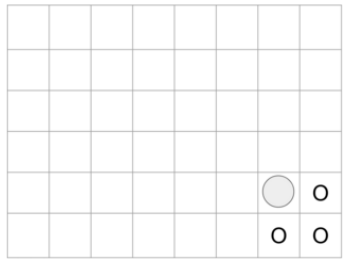
마지막으로, 다음 그림과 같이 \(N = 6, M = 8, K = 0\)이고 막혀 있는 칸이 없는 보드를 생각하자. 이 보드에서 (1, 1)에 놓인 말이 움직일 수 있는 칸은 총 2개로 다음 그림에 \(\bigcirc\) 표시된 것과 같다.

게임의 목표는 말을 보드의 맨 오른쪽 아래 칸, 즉, \((N, M)\)으로 옮기는 것이고, 마지막으로 말을 움직인 사람이 이긴다. 한국이와 정올이 모두 최선을 다해 게임에 임한다고 가정하자.

게임을 시작하는 위치(초기에 말이 놓여 있는 위치)에 따라 게임의 승자가 달라질 수 있다. \(Q\)개의 보드 상의 위치 \((x_1, y_1),(x_2, y_2), · · · ,(x_Q, y_Q)\)가 주어질 때 각 위치에서 게임을 시작할 때의 승자를 구하여라.

첫 번째 줄에 세 정수 \(N, M, K\)가 공백을 사이에 두고 주어진다

이후 \(N\)개의 줄에 걸쳐 #과 .으로만 구성된 길이 \(M\)의 문자열이 한 줄에 하나씩 주어진다. \(1 \le i \le N\) 과 \(1 \le j \le M\)에 대해, \(i\)번째 줄의 \(j\)번째 문자가 ‘#’ 이면 \((i, j)\)가 막혀 있는 칸임을, ‘.’이면 막혀 있지 않은 칸임을 의미한다. 

그 다음 줄에 정수 \(Q\)가 주어진다.

다음 \(Q\)개의 줄 중 \(i(1 \le i \le Q)\)번째 줄에는 정수 \(x_i\)와 \(y_i\)가 공백을 사이에 두고 주어진다

제약 조건

• \(2 \le N \le 300\)
• \(2 \le M \le 300\)
• \(K \ge 0\)
• \(K \le N − 1\)
• \(K \le M − 1\)
• \((N, M)\) 칸은 막혀 있지 않다.
• 임의의 막혀 있지 않은 칸에서 시작해서 말을 규칙에 따라 \((N, M)\)으로 옮길 수 있다.
• \(1 \le Q \le 300\)
• 모든 \(i (1 \le i \le Q)\)에 대해:
• \(1 \le x_i \le N, 1 \le y_i \le M\)
• \((x_i, y_i)\) 칸은 막혀 있지 않다. \((x_i, y_i)\)는 (N, M)이 아니다. 

부분문제

1. (5점) \(K = 0.\)
2. (17점) \(N = M\)이며 \(K \ge 1\)이고, \(i \neq j\) 인 \((i, j)\) 칸들은 전부 막혀 있다.
3. (25점) 막혀 있는 칸이 없다.
4. (53점) 추가 제약 조건 없음.