\(N\)개의 자연수가 좌우 일렬로 놓여 있다. 왼쪽에서 \(i (1 \le i \le N)\)번째에 놓여 있는 자연수는 \(A_i\)다. 

여러분은 이 중 몇 개의 자연수를 원하는 만큼 고를 수 있다. 단, 아무 자연수도 고르지 않는 것은 허용되지 않으며, 반드시 1개 이상의 자연수를 골라야 한다

여러분이 고른 자연수의 개수를 \(k\)라고 하고, 고른 자연수들을 \(B_1, B_2, · · ·, B_k\)라고 하자. 고른 자연수들의 순서는 기존에 놓여 있던 순서 그대로 유지된다. 

예를 들어, \(N = 5, A = [3, 1, 4, 1, 5]\)라고 하자. 여러분이 왼쪽에서 두 번째, 네 번째, 다섯 번째에 놓여 있는 자연수를 고르면, \(k = 3\)이고, \(B = [1, 1, 5]\)가 된다.

\(B\)의 첫 번째 자연수와 두 번째 자연수의 합, 두 번째 자연수와 세 번째 자연수의 합, 세 번째 자연수와 네 번째 자연수의 합, . . . 과 같이, 이웃한 두 자연수의 합을 구했을 때, 항상 홀수라면, \(B\)를 불안정한 수열이라고 하자. \(k = 1\)이면 특별히 B는 불안정한 수열이라고 본다.

예를 들어, \(k = 6, B = [1, 4, 3, 2, 5, 4]\)라면, \(B\)의 첫 번째 자연수(1)와 두 번째 자연수(4)의 합은 5로 홀수이고, 두 번째 자연수(4)와 세 번째 자연수(3)의 합은 7로 홀수이고, 세 번째 자연수(3)와 네 번째 자연수 (2)의 합은 5로 홀수이고, 네 번째 자연수(2)와 다섯 번째 자연수(5)의 합은 7로 홀수이고, 다섯 번째 자연수 (5)와 여섯 번째 자연수(4)의 합은 9로 홀수이므로, 이웃한 두 자연수의 합이 항상 홀수라서, \(B\)는 불안정한 수열이다.

또한, \(k = 1, B = [2]\)라면, \(k = 1\)이므로, \(B\)는 불안정한 수열이다

하지만, \(k = 4, B = [4, 5, 1, 2]\)라면, \(B\)의 첫 번째 자연수(4)와 두 번째 자연수(5)의 합은 9로 홀수이지만, 두 번째 자연수(5)와 세 번째 자연수(1)의 합은 6으로 짝수이므로, 이웃한 두 자연수의 합이 홀수가 아닌 경우가 있어서, \(B\)는 불안정한 수열이 아니다.

여러분은 \(B\)가 불안정한 수열이 되도록 하면서, 가장 많은 개수의 자연수를 골라야 한다. 이 때, 최대 몇 개의 자연수를 고를 수 있는지 구하는 프로그램을 작성하라.

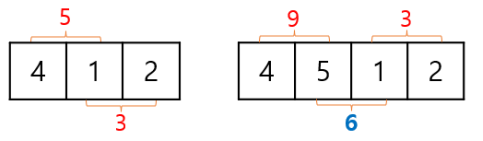
예를 들어, \(A = [4, 5, 1, 2]\)일 때를 살펴보자. 만약 모든 자연수를 고르면 \(B = [4, 5, 1, 2]\)가 되고, 이는 불안정한 수열이 아니므로, 4개의 자연수를 골라서 불안정한 수열을 만들 수는 없다. 하지만, 왼쪽에서 첫 번째, 세 번째, 네 번째에 놓여 있는 자연수를 고르면 \(B = [4, 1, 2]\)가 되고, \(B\)의 첫 번째 자연수(4)와 두 번째 자연수(1)의 합은 5로 홀수이고, 두 번째 자연수(1)와 세 번째 자연수(2)의 합은 3으로 홀수이므로, 이웃한 두 자연수의 합이 항상 홀수라서, \(B\)는 불안정한 수열이다. 따라서, 3개의 자연수를 골라서 불안정한 수열을 만들 수 있으며, 이것이 최대이다.

첫 번째 줄에 \(N\)이 주어진다.

두 번째 줄에 \(A_1, A_2, · · · , A_N\)이 공백을 사이에 두고 차례대로 주어진다.

제약 조건

• 주어지는 모든 수는 자연수다.
• \(1 \le N \le 300 000\)
• \(1 \le Ai \le 100 000 (1 \le i \le N)\)

부분문제

1. (5점) 정답은 \(N − 1\) 또는 \(N\)이다.
2. (8점) \(N \le 15\)
3. (12점) \(N \le 5 000\)
4. (15점) \(A_i \le 50 (1 \le i \le N)\)
5. (60점) 추가 제약 조건 없음.