KOI 호숫가에 여러 개미가 모여 사는 개미굴이 있다. 개미굴은 둥근 호수의 둘레를 따라 1부터 $N$까지의 번호가 붙은 $N$개의 방이 차례대로 원형으로 배치되어 있으며, 모든 $i(1\le i\le N-1)$에 대해 $i$번째 방과 $i+1$번째 방이, 그리고 $N$번째 방과 1번째 방이 통로로 직접 연결되어 있는 형태였다. 

하지만 여러 이유로 인해 각 방에서 몇 개의 쪽방이 갈라지기 시작해서, 현재는 모든 $i(1\le i\le N)$에 대해, 개미굴의 $i$번째 방에 $C_i$개의 쪽방이 통로로 직접 연결되어 있다. $i$번째 방과 연결된 쪽방은 $i$번째 방 이외에 다른 방과 통로로 연결되어 있지 않다. 예를 들어 $N=7$이고, $C=[3,0,0,1,0,2,0]$인 개미굴은 아래 그림과 같은 형태이다.

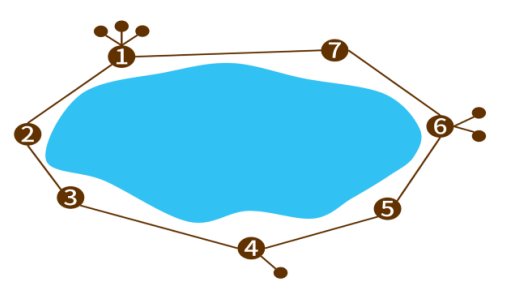
개미굴의 각 방과 쪽방에는 최대 한 마리의 개미가 살 수 있다. 만약 통로로 직접 연결되어 있는 두 곳(방 또는 쪽방) 모두에 개미가 살고 있다면, 두 개미는 서로 불편해한다. 이러한 불편함을 방지하기 위해, 현재 개미굴의 각 통로가 직접 연결하는 두 곳 중 최대 한 곳에만 개미가 살고 있다.

개미들은 똑똑하기 때문에, 이 조건을 만족하는 하에 최대한 많은 수의 개미들이 현재 개미굴에 살고 있다고 한다. 현재 개미굴의 구조가 주어질 때, 개미굴에 살고 있는 개미의 수를 구하는 프로그램을 작성하라. 

첫 번째 줄에 정수 $N$이 주어진다.

두 번째 줄에 각 방과 연결된 쪽방의 개수를 의미하는 $N$개의 정수 $C_1,C_2,···,C_N$이 공백으로 구분되어 주어진다.

제약 조건

• 주어지는 모든 수는 정수이다.
• $2\le N\le 250000$
• $0\le C_i\le {10}^{12}$(모든 $1\le i\le N)$

부분문제

1. (4점) $N=2$
2. (8점) $N\le 1000$이고, $C_i=0$ (모든 $1\le i\le N$)
3. (14점) $N\le 1000$이고, $C_i\le 1$ (모든 $1\le i\le N$)
4. (15점) $N\le 1000$
5. (20점) $C_i\le 1$ (모든 $1\le i\le N$)
6. (13점) $C_i\le 1000$ (모든 $1\le i\le N$)
7. (9점) $C_i\ge 1$ (모든 $1\le i\le N$)
8. (17점) 추가 제약 조건 없음.