문제 설명
모든 노드의 자식 노드가 0개 또는 2개인 이진 트리 \(T\)에 대해 \(S(T)\)의 값은 다음과 같이 정의한다.
- \(T\)에서 노드 \(u\)를 루트로 하는 서브 트리는, \(u\)와 \(u\)의 자손 노드들로만 구성된 집합이다.
- \(T\)의 중위 순회 수열 \(p(T)\)는 \(T\)를 중위 순회하면서 방문하는 노드들을 순서대로 나열한 수열로, 아래와 같이 정의할 수 있다.
- \(T\)의 루트 노드를 \(r\)이라 하자. \([r]\)을 \(r\) 하나로만 구성된 길이 \(1\)의 수열이라고 하자.
- 만약 \(r\)의 자식 노드가 0개라면, \(p(T)\)는 \([r]\)이다.
- 만약 \(r\)의 자식 노드가 2개라면, \(r\)의 왼쪽 자식 노드를 루트로 하는 서브 트리가 \(X, r\)의 오른쪽 자식 노드를 루트로 하는 서브 트리가 \(Y\) 일 때, \(p(T)\)는 \(p(X), [r], p(Y )\)을 순서대로 이어붙인 수열이다.
- \(T\)의 리프 노드 개수를 \(k\)라고 하자. \(T\)의 리프 노드들에 \(1, 2, · · · , k\)의 번호를 \(p(T)\)에서 나타나는 순서대 로 (즉, 중위 순회 방문 순서대로) 붙였다고 하자.
- \(T\)의 서브 트리를 선택하면, 해당 서브 트리에 포함된 리프 노드들이 덮인다고 하자.
- \(1 \le a \le b \le k\)일 때, \(f(a, b)\)는 리프 노드들 중 번호가 \(a\) 이상 \(b\) 이하인 리프 노드들만을 덮고 다른 리프 노드들은 덮지 않기 위해, \(T\)에서 선택해야 하는 최소 서브 트리 개수이다.
- \(S(T)\)의 값은 \(1 \le a \le b \le k\)인 모든 \((a, b)\) 정수 순서쌍에 대한 \(f(a, b)\)의 합을 \(10^9+7\)로 나눈 나머지이다
예를 들어, 다음과 같은 이진 트리 \(T\)가 있다고 가정해보자.
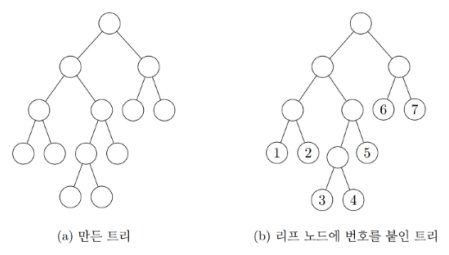 \(f(5, 7)\)의 값은 2이다. 다음과 같이 서브 트리 두 개를 선택하면 5, 6, 7번 리프 노드만 덮이기 때문이다.
\(f(5, 7)\)의 값은 2이다. 다음과 같이 서브 트리 두 개를 선택하면 5, 6, 7번 리프 노드만 덮이기 때문이다.
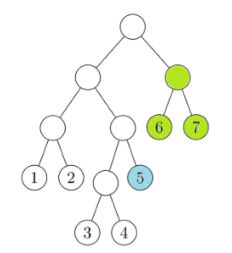 이런 식으로 모든 \(1 \le a \le b \le 7\)에 대해 \(f(a, b)\)의 값의 합은 47이고, 이를 \(10^9 + 7\)로 나눈 나머지를 구하면 \(S(T) = 47\)이다.
이런 식으로 모든 \(1 \le a \le b \le 7\)에 대해 \(f(a, b)\)의 값의 합은 47이고, 이를 \(10^9 + 7\)로 나눈 나머지를 구하면 \(S(T) = 47\)이다.
정수열 \(A_1, A_2, · · · , A_N\)과 \(B_1, B_2, · · · , B_N\)이 주어진다.
이진 트리 \(T_0, T_1, · · · , T_N\)을 다음과 같이 정의한다
\(S(T_1), S(T_2), · · · , S(T_N )\)을 구하는 프로그램을 작성하라.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(1 \le N \le 100 000\)
• \(0 \le A_i \le i − 1 (1 \le i \le N)\)
•\( 0 \le B_i \le i − 1 (1 \le i \le N)\)
부분문제
1. (5점) \(A_i = B_i = i − 1 (1 \le i \le N), N \le 10\)
2. (10점) \(A_i = B_i = i − 1 (1 \le i \le N)\)
3. (5점) \(A_i = i − 1, B_i = 0 (1 \le i \le N)\)
4. (10점) \(T_1, T_2, · · · , T_N\)의 노드 개수의 합은 1 000 이하
5. (25점) \(T_1, T_2, · · · , T_N\)의 노드 개수의 합은 300 000 이하
6. (45점) 추가 제약 조건 없음.


정수열 \(A_1, A_2, · · · , A_N\)과 \(B_1, B_2, · · · , B_N\)이 주어진다.
이진 트리 \(T_0, T_1, · · · , T_N\)을 다음과 같이 정의한다
-
\(T_0\) 은 노드가 1개인 트리
-
\(T_i\) 는 루트의 왼쪽 자식 노드를 루트로 하는 서브 트리가 \(T_{A_i}\)이고, 루트의 오른쪽 자식 노드를 루트로
하는 서브 트리가 \(T_{B_i}\)인 트리 \((1 \le i \le N, 0 \le A_i \le i − 1, 0 \le B_i \le i − 1)\)
\(S(T_1), S(T_2), · · · , S(T_N )\)을 구하는 프로그램을 작성하라.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(1 \le N \le 100 000\)
• \(0 \le A_i \le i − 1 (1 \le i \le N)\)
•\( 0 \le B_i \le i − 1 (1 \le i \le N)\)
부분문제
1. (5점) \(A_i = B_i = i − 1 (1 \le i \le N), N \le 10\)
2. (10점) \(A_i = B_i = i − 1 (1 \le i \le N)\)
3. (5점) \(A_i = i − 1, B_i = 0 (1 \le i \le N)\)
4. (10점) \(T_1, T_2, · · · , T_N\)의 노드 개수의 합은 1 000 이하
5. (25점) \(T_1, T_2, · · · , T_N\)의 노드 개수의 합은 300 000 이하
6. (45점) 추가 제약 조건 없음.
입력 설명
첫 번째 줄에 정수 \(N\)이 주어진다.
다음 \(N\)개의 줄 중 \(i (1 \le i \le N)\)번째 줄에는 \(A_i\)와 \(B_i\)가 공백으로 구분되어 주어진다.
다음 \(N\)개의 줄 중 \(i (1 \le i \le N)\)번째 줄에는 \(A_i\)와 \(B_i\)가 공백으로 구분되어 주어진다.
출력 설명
\(N\)개의 줄을 출력한다. \(i (1 \le i \le N)\)번째 줄에는 \(S(Ti)\)를 출력해야 한다
입력 예시 Copy
5
0 0
1 0
1 2
3 1
4 4
출력 예시 Copy
3
7
21
47
254
도움
중3,고2