문제 설명
당신은 친구인 다빈과 함께 아래와 같이 무한히 긴 수직선 위에서 보물찾기 놀이를 하고 있다
 먼저 당신은 수직선에 있는 서로 다른 두 위치 \(L, R\)에 보물 두 개를 숨긴다. \((L < R)\) 아래는 숨긴 두
보물의 위치가 \(L = −2, R = 3\)인 경우의 예시이다. 주황색으로 표시된 두 개의 칸에 보물이 숨겨져 있다.
먼저 당신은 수직선에 있는 서로 다른 두 위치 \(L, R\)에 보물 두 개를 숨긴다. \((L < R)\) 아래는 숨긴 두
보물의 위치가 \(L = −2, R = 3\)인 경우의 예시이다. 주황색으로 표시된 두 개의 칸에 보물이 숨겨져 있다.
 당신이 보물 두 개를 숨긴 다음, 다빈이 보물을 찾기 시작한다. 다빈은 당신이 정한 시작 위치 \(S\)에서 시작해,
아래 단계들을 순서대로 수행하며 보물을 찾을 것이다. 시작 위치 \(S\)는 항상 두 보물의 위치 \(L\)과 \(R\) 사이에
있다. \((L < S < R)\) 두 보물 중 하나의 보물을 찾으면 보물찾기 놀이가 끝난다.
당신이 보물 두 개를 숨긴 다음, 다빈이 보물을 찾기 시작한다. 다빈은 당신이 정한 시작 위치 \(S\)에서 시작해,
아래 단계들을 순서대로 수행하며 보물을 찾을 것이다. 시작 위치 \(S\)는 항상 두 보물의 위치 \(L\)과 \(R\) 사이에
있다. \((L < S < R)\) 두 보물 중 하나의 보물을 찾으면 보물찾기 놀이가 끝난다.
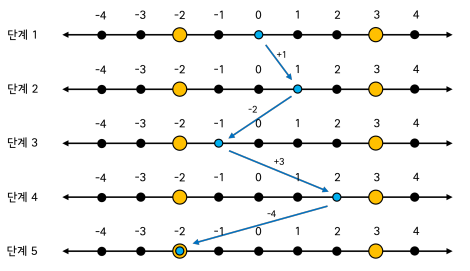 5번째 단계에서 조사한 위치 −2에 보물이 있으므로, 5번째 단계에서 보물찾기 놀이가 끝난다.
5번째 단계에서 조사한 위치 −2에 보물이 있으므로, 5번째 단계에서 보물찾기 놀이가 끝난다.
당신이 정하는 세 변수 \(L, R, S\)의 값에 따라서, 보물찾기 놀이가 끝나는 단계가 달라진다. 따라서, 당신은 세 변수 값의 조합을 여러 가지 시도해 보려 한다.
각 경우에 대해, 두 보물의 위치 \(L, R\)과 다빈이 시작하는 위치 \(S\)가 주어졌을 때, 몇 번째 단계에서 보물찾기 놀이가 끝나는지 구하여라.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(1 \le T \le 10 000\)
• \(−100 000 000 \le L < S < R \le 100 000 000\)
부분 문제
1. (8점) \(T = 1, R = 1, S = 0\)
2. (9점) \(T = 1, L = −1, S = 0\)
3. (15점) \(−1 000 \le L \le −1, 1 \le R \le 1 000, S = 0\)
4. (16점) \(−1 000 \le L < S < R \le 1 000\)
5. (52점) 추가 제약 조건 없음.


- 위치 \(S\)를 조사한다.
- 오른쪽으로 1칸 이동해, 위치 \(S + 1\)를 조사한다.
- 왼쪽으로 2칸 이동해, 위치 \(S + 1 − 2\)를 조사한다.
- 오른쪽으로 3칸 이동해, 위치 \(S + 1 − 2 + 3\)를 조사한다.
- 왼쪽으로 4칸 이동해, 위치 \(S + 1 − 2 + 3 − 4\)를 조사한다.
- 오른쪽으로 5칸 이동해, 위치 \(S + 1 − 2 + 3 − 4 + 5\)를 조사한다.
- . .

당신이 정하는 세 변수 \(L, R, S\)의 값에 따라서, 보물찾기 놀이가 끝나는 단계가 달라진다. 따라서, 당신은 세 변수 값의 조합을 여러 가지 시도해 보려 한다.
각 경우에 대해, 두 보물의 위치 \(L, R\)과 다빈이 시작하는 위치 \(S\)가 주어졌을 때, 몇 번째 단계에서 보물찾기 놀이가 끝나는지 구하여라.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(1 \le T \le 10 000\)
• \(−100 000 000 \le L < S < R \le 100 000 000\)
부분 문제
1. (8점) \(T = 1, R = 1, S = 0\)
2. (9점) \(T = 1, L = −1, S = 0\)
3. (15점) \(−1 000 \le L \le −1, 1 \le R \le 1 000, S = 0\)
4. (16점) \(−1 000 \le L < S < R \le 1 000\)
5. (52점) 추가 제약 조건 없음.
입력 설명
첫 번째 줄에 당신이 시도해 볼 경우의 수 \(T\)가 주어진다. 이후 \(T\)개의 줄에, 각 경우에 대해 세 변수 \(L, R,
S\)의 값이 공백으로 구분되어 주어진다.
출력 설명
\(T\)개의 줄에 걸쳐, 각 경우에 몇 번째 단계에서 보물찾기 놀이가 끝나는지 출력한다.
입력 예시 Copy
2
-2 3 0
4 8 6
출력 예시 Copy
5
4
도움
(초1)
첫 번째 경우 \((L = −2, R = 3, S = 0)\)는 위의 그림에 설명되어 있다.
두 번째 경우 \((L = 4, R = 8, S = 6)\)에서 다빈은 아래와 같은 과정으로 보물을 찾게 된다.
첫 번째 경우 \((L = −2, R = 3, S = 0)\)는 위의 그림에 설명되어 있다.
두 번째 경우 \((L = 4, R = 8, S = 6)\)에서 다빈은 아래와 같은 과정으로 보물을 찾게 된다.
- 위치 6을 조사한다.
- 오른쪽으로 1칸 이동해, 위치 6 + 1 = 7을 조사한다.
- 왼쪽으로 2칸 이동해, 위치 7 − 2 = 5를 조사한다.
- 오른쪽으로 3칸 이동해, 위치 5 + 3 = 8을 조사한다.