문제 설명
수직선 도로 위에 \(N\) 개의 가로등이 켜져 있다. 각 가로등의 위치는 왼쪽부터 차례대로 \(A_1 < · · · < A_N\)로
나타낼 수 있다.
위치 \(x\)의 어두운 정도를, 그 위치로부터 가장 가까운 가로등까지의 거리로 정의하자. 이는 \(N\) 개의 수 \(|A_1 − x|, · · · , |A_N − x|\) 중에서 가장 작은 값과 같다. 여기서, \(| · |\)는 절댓값 기호로, \(y \ge 0\)이면 \(|y| := y, y < 0\) 이면 \(|y| := −y\)이다.
예를 들어, \(N = 3\) 개의 가로등이 차례대로 \(A_1 = 1, A_2 = 4, A_3 = 8\)에 위치한다면, 0부터 10까지 각 정수 위치의 어두운 정도는 다음과 같다.
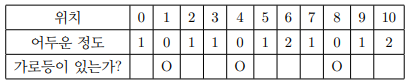\(x = 0\)부터 \(x = L\)까지 \(L + 1\) 개의 정수 위치의 어두운 정도를 모두 계산했을 때, 가장 작은 값부터 \(K\) 번째로 작은 값까지 차례대로 출력하는 프로그램을 작성하라.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(1 \le L \le 1 000 000 000 000 000 000\)
• \(1 \le N \le 300 000\)
• \(1 \le K \le 500 000\)
• \(K \le L + 1\)
• \(0 \le A_1 < A_2 < · · · < A_N \le L\)
부분 문제
1. (10점) \(N = 1\)
2. (20점) \(N \le 2 500, L \le 2 500\)
3. (15점) \(2 \le N. N − 1\)은 \(L\)을 나눈다. \(A_i = \frac{L} {N−1} \times (i − 1)\)
4. (20점) \(L \le 5 000 000\)
5. (35점) 추가 제약 조건 없음.
위치 \(x\)의 어두운 정도를, 그 위치로부터 가장 가까운 가로등까지의 거리로 정의하자. 이는 \(N\) 개의 수 \(|A_1 − x|, · · · , |A_N − x|\) 중에서 가장 작은 값과 같다. 여기서, \(| · |\)는 절댓값 기호로, \(y \ge 0\)이면 \(|y| := y, y < 0\) 이면 \(|y| := −y\)이다.
예를 들어, \(N = 3\) 개의 가로등이 차례대로 \(A_1 = 1, A_2 = 4, A_3 = 8\)에 위치한다면, 0부터 10까지 각 정수 위치의 어두운 정도는 다음과 같다.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(1 \le L \le 1 000 000 000 000 000 000\)
• \(1 \le N \le 300 000\)
• \(1 \le K \le 500 000\)
• \(K \le L + 1\)
• \(0 \le A_1 < A_2 < · · · < A_N \le L\)
부분 문제
1. (10점) \(N = 1\)
2. (20점) \(N \le 2 500, L \le 2 500\)
3. (15점) \(2 \le N. N − 1\)은 \(L\)을 나눈다. \(A_i = \frac{L} {N−1} \times (i − 1)\)
4. (20점) \(L \le 5 000 000\)
5. (35점) 추가 제약 조건 없음.
입력 설명
첫 줄에 세 정수 \(L, N, K\)가 공백으로 구분되어 차례대로 주어진다.
그다음 줄에 \(N\) 개의 정수 \(A_1, · · · , A_N\)이 공백으로 구분되어 차례대로 주어진다
그다음 줄에 \(N\) 개의 정수 \(A_1, · · · , A_N\)이 공백으로 구분되어 차례대로 주어진다
출력 설명
첫 줄부터 \(K\) 개의 줄에 걸쳐 답을 출력한다. 이 중 \(i\) 번째 줄에는 \(i\) 번째로 작은 어두운 정도의 값을
출력한다.
입력 예시 Copy
10 3 4
1 4 8
출력 예시 Copy
0
0
0
1
도움
(초2,중1,고1)