문제 설명
\(2N\)개의 공과 \(N + 1\)개의 상자가 있다. 공들의 색깔은 \(1, 2, · · · , N\) 중 하나이며, 각 색깔에 대해 그 색깔로
칠해진 공은 정확히 \(2\)개 있다. 각 상자는 공을 최대 \(2\)개까지 가지고 있을 수 있다. 처음에는 첫 번째 상자부터 \(N\)번째 상자에 각각 \(2\)개의 공이 들어 있고, \(N + 1\)번째 상자는 비어 있다. \(i\)번째 상자의 위에 있는 공의 색깔은 \(A_i\)이고, 아래에 있는 공의 색깔은 \(B_i\)이다.
한 상자에서 다른 상자로 공을 옮길 수 있는데, 상자의 가장 위에 있는 공을 빼서 다른 상자의 가장 위에 넣는 작업을 할 수 있다.
여러분은 같은 색으로 칠해진 \(2\)개의 공이 같은 상자에 들어가도록 공을 옮겨야 한다. 이때, 공을 옮기는 작업을 할 때마다 다음 두 조건 중 하나를 만족해야 한다.
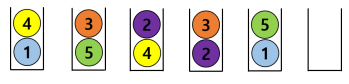 예를 들어, 위 그림에서 아래와 같이 공을 옮기면 \(6\)번의 이동으로 색깔이 같은 공이 같은 상자에 들어가게
되고, 공을 \(6\)번보다 적게 옮겨서 목표를 달성하는 것은 불가능하다.
예를 들어, 위 그림에서 아래와 같이 공을 옮기면 \(6\)번의 이동으로 색깔이 같은 공이 같은 상자에 들어가게
되고, 공을 \(6\)번보다 적게 옮겨서 목표를 달성하는 것은 불가능하다.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(1 \le N \le 200 000\)
• \(1 \le A_i , B_i \le N\)
• 각 \(i (1 \le i \le N)\)에 대해서 \(A_1, A_2, · · · , A_N , B_1, B_2, · · · , B_N\)중 정확히 \(2\)개의 값이 \(i\)와 같다.
부분 문제
1. (2점) \(N \le 2\)
2. (23점) \(N \le 20\)
3. (15점) 색이 같은 공이 같은 상자에 들어가도록 공을 옮기는 방법이 존재한다.
4. (15점) \(N \le 2 000\)
5. (45점) 추가 제약 조건 없음.
한 상자에서 다른 상자로 공을 옮길 수 있는데, 상자의 가장 위에 있는 공을 빼서 다른 상자의 가장 위에 넣는 작업을 할 수 있다.
여러분은 같은 색으로 칠해진 \(2\)개의 공이 같은 상자에 들어가도록 공을 옮겨야 한다. 이때, 공을 옮기는 작업을 할 때마다 다음 두 조건 중 하나를 만족해야 한다.
- 옮겨서 공을 놓으려는 상자가 완전히 비어 있어야 한다.
- 옮겨서 공을 놓으려는 상자에 공이 정확히 하나 들어 있고, 이동하려는 공과 해당 상자에 있는 공의 색깔이 같아야 한다.

- 네 번째 상자의 색깔이 \(3\)인 공을 여섯 번째 상자로 옮긴다.
- 세 번째 상자의 색깔이 \(2\)인 공을 네 번째 상자로 옮긴다.
- 첫 번째 상자의 색깔이 \(4\)인 공을 세 번째 상자로 옮긴다.
- 두 번째 상자의 색깔이 \(3\)인 공을 여섯 번째 상자로 옮긴다.
- 다섯 번째 상자의 색깔이 \(5\)인 공을 두 번째 상자로 옮긴다.
- 다섯 번째 상자의 색깔이 \(1\)인 공을 첫 번째 상자로 옮긴다.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(1 \le N \le 200 000\)
• \(1 \le A_i , B_i \le N\)
• 각 \(i (1 \le i \le N)\)에 대해서 \(A_1, A_2, · · · , A_N , B_1, B_2, · · · , B_N\)중 정확히 \(2\)개의 값이 \(i\)와 같다.
부분 문제
1. (2점) \(N \le 2\)
2. (23점) \(N \le 20\)
3. (15점) 색이 같은 공이 같은 상자에 들어가도록 공을 옮기는 방법이 존재한다.
4. (15점) \(N \le 2 000\)
5. (45점) 추가 제약 조건 없음.
입력 설명
첫 번째 줄에 \(N\)이 주어진다.
두 번째 줄부터 \(N\)개의 줄에 걸쳐 각 상자에 들어 있는 두 공들의 색깔이 주어진다. \(N\)개의 줄 중 \(i\)번째 줄에는 \(A_i , B_i\)가 공백으로 구분되어 주어진다.
두 번째 줄부터 \(N\)개의 줄에 걸쳐 각 상자에 들어 있는 두 공들의 색깔이 주어진다. \(N\)개의 줄 중 \(i\)번째 줄에는 \(A_i , B_i\)가 공백으로 구분되어 주어진다.
출력 설명
첫 번째 줄에 색깔이 같은 공이 같은 상자에 들어가도록 하기 위해 필요한 공의 이동 횟수의 최솟값을
출력한다.
단, 불가능하다면 \(−1\)을 출력한다.
단, 불가능하다면 \(−1\)을 출력한다.
입력 예시 Copy
5
4 1
3 5
2 4
3 2
5 1
출력 예시 Copy
6
도움
(초3,중2)