문제 설명
KOI 공원은 \(1\)번 지점부터 \(N\)번 지점까지 \(N\)개의 지점으로 구성되어 있으며, 두 지점을 잇는 \(N − 1\)개의
도로가 있다. \(i\)번째 도로는 \(U_i\)번 지점과 \(V_i\)번 지점을 이으며, 점수 \(W_i\)를 가진다\((1 \le i \le N − 1)\).
KOI 공원에서는 어떤 두 지점이든 도로를 따라 서로 이동할 수 있다. 즉, KOI 공원은 트리 구조를 이룬다.
KOI 공원에서 점수 경주를 하려고 한다. 점수 경주는 다음과 같이 이루어진다.
\(i\)번 지점에 대해, 해당 지점이 시작 지점일 때 최적 전략을 따랐을 때 참가자들의 최종 점수의 총합을 \(S_i\) 라고 하자. 또한 그때 참가자들이 자신의 점수를 \(0\)점으로 바꾼 횟수의 총합을 \(C_i\)라고 하자.
예를 들어, KOI 공원의 모습이 다음과 같을 때, \(1\)번 지점이 시작 지점인 경우를 생각해 보자.
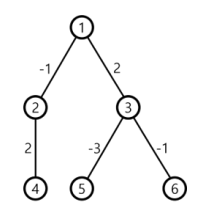 최적 전략을 따를 때, 점수 경주의 과정은 다음과 같다.
최적 전략을 따를 때, 점수 경주의 과정은 다음과 같다.
\(S_1, · · · , S_N\) 및 \(C_1, · · · , C_N\)을 구하는 프로그램을 작성하라.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(2 \le N \le 300 000\)
• \(1 \le U_i , V_i \le N (1 \le i \le N − 1)\)
• \(−10 000 000 \le W_i \le 10 000 000 (1 \le i \le N − 1)\)
부분문제
1. (2점) \(N \le 1 000\)
2. (6점) \(0 \le W_i \le 5 (1 \le i \le N − 1)\)
3. (20점) 0 \le W_i \le 5 또는 W_i \le −1 000 000 (1 \le i \le N − 1)\)
4. (4점) \(U_i = 1, V_i = i + 1 (1 \le i \le N − 1)\)
5. (10점) \(U_i = i, V_i = i + 1 (1 \le i \le N − 1)\)
6. (16점) \(U_i = \lfloor\frac{i+1}{2}\rfloor, V_i = i + 1 (1 \le i \le N − 1)\)
7. (18점) 세 개 이상의 다른 지점과 도로로 연결된 지점은 최대 두 개이다.
8. (24점) 추가 제약 조건 없음.
각 부분문제에 대해, \(S_1, · · · , S_N\)만을 구한 경우 해당 부분문제의 점수의 절반을 얻을 수 있다. 그 방법에 대
해서는 출력 형식을 참고하라.\(S_1, · · · , S_N\) 및 \(C_1, · · · , C_N\)을 구한 경우, \(S_1, · · · , S_N\)이 정확해도 \(C_1, · · · , C_N\) 이 정확하지 않다면 점수를 받을 수 없음에 유의하라.
KOI 공원에서는 어떤 두 지점이든 도로를 따라 서로 이동할 수 있다. 즉, KOI 공원은 트리 구조를 이룬다.
KOI 공원에서 점수 경주를 하려고 한다. 점수 경주는 다음과 같이 이루어진다.
- 총 \(N −1\)명의 참가자가 시작 지점에서 출발해, 각자 시작 지점을 제외한 서로 다른 \(N −1\)개의 지점으로 단순 경로를 따라 이동한다.
- 각 참가자는 처음에 \(0\)점의 점수를 가지고 있다.
- 각 도로에 대해, 해당 도로를 지나면 그 도로의 점수만큼 점수를 받게 된다.
- 참가자들은 어떤 지점에서든 자신의 점수를 \(0\)점으로 만들 수 있다. 자신의 목표 지점으로 도착한 후에도 가능하다.
\(i\)번 지점에 대해, 해당 지점이 시작 지점일 때 최적 전략을 따랐을 때 참가자들의 최종 점수의 총합을 \(S_i\) 라고 하자. 또한 그때 참가자들이 자신의 점수를 \(0\)점으로 바꾼 횟수의 총합을 \(C_i\)라고 하자.
예를 들어, KOI 공원의 모습이 다음과 같을 때, \(1\)번 지점이 시작 지점인 경우를 생각해 보자.

- \(2\)번 지점이 목표 지점인 참가자는 \(2\)번 지점으로 이동하며 \(−1\)점을 받게 된다. 이후 \(2\)번 지점에서 자신의 점수를 \(0\)점으로 만든다. 최종 점수는 \(0\)점이다.
- \(3\)번 지점이 목표 지점인 참가자는 \(3\)번 지점으로 이동하며 \(2\)점을 받게 된다. 최종 점수는 \(2\)점이다.
- \(4\)번 지점이 목표 지점인 참가자는 \(2\)번 지점으로 이동하며 \(−1\)점을 받는다. 이후 \(2\)번 지점에서 자신의 점수를 \(0\)점으로 만든다. 이후 \(4\)번 지점으로 이동하며 \(2\)점을 받게 된다. 최종 점수는 \(2\)점이다.
- \(5\)번 지점이 목표 지점인 참가자는 \(3\)번 지점으로 이동하며 \(2\)점을 받는다. 이후 \(5\)번 지점으로 이동하며 \(−3\)점을 받는다. 이후 \(5\)번 지점에서 자신의 점수를 \(0\)점으로 만든다. 최종 점수는 \(0\)점이다.
- \(6\)번 지점이 목표 지점인 참가자는 \(3\)번 지점으로 이동하며 \(2\)점을 받는다. 이후 \(6\)번 지점으로 이동하며 \(−1\)점을 받게 된다. 최종 점수는 \(1\)점이다.
\(S_1, · · · , S_N\) 및 \(C_1, · · · , C_N\)을 구하는 프로그램을 작성하라.
제약 조건
• 주어지는 모든 수는 정수이다.
• \(2 \le N \le 300 000\)
• \(1 \le U_i , V_i \le N (1 \le i \le N − 1)\)
• \(−10 000 000 \le W_i \le 10 000 000 (1 \le i \le N − 1)\)
부분문제
1. (2점) \(N \le 1 000\)
2. (6점) \(0 \le W_i \le 5 (1 \le i \le N − 1)\)
3. (20점) 0 \le W_i \le 5 또는 W_i \le −1 000 000 (1 \le i \le N − 1)\)
4. (4점) \(U_i = 1, V_i = i + 1 (1 \le i \le N − 1)\)
5. (10점) \(U_i = i, V_i = i + 1 (1 \le i \le N − 1)\)
6. (16점) \(U_i = \lfloor\frac{i+1}{2}\rfloor, V_i = i + 1 (1 \le i \le N − 1)\)
7. (18점) 세 개 이상의 다른 지점과 도로로 연결된 지점은 최대 두 개이다.
8. (24점) 추가 제약 조건 없음.
각 부분문제에 대해,
입력 설명
첫 번째 줄에 \(N\)이 주어진다.
이후 \(N − 1\)개의 줄에 걸쳐 \(i\)번째 줄에는 \(U_i , V_i , W_i\)가 공백으로 구분되어 주어진다.
이후 \(N − 1\)개의 줄에 걸쳐 \(i\)번째 줄에는 \(U_i , V_i , W_i\)가 공백으로 구분되어 주어진다.
출력 설명
\(S_1, · · · , S_N\)만을 구한 경우
• 첫 번째 줄에 \(0\)을 출력한다.
• 두 번째 줄에 \(S_1, · · · , S_N\)을 공백으로 구분하여 출력한다.
\( S_1, · · · , S_N\) 및 \(C_1, · · · , C_N\)을 구한 경우
• 첫 번째 줄에 \(1\)을 출력한다.
• 두 번째 줄에 \(S_1, · · · , S_N\)을 공백으로 구분하여 출력한다.
• 세 번째 줄에 \(C_1, · · · , C_N\)을 공백으로 구분하여 출력한다.
• 첫 번째 줄에 \(0\)을 출력한다.
• 두 번째 줄에 \(S_1, · · · , S_N\)을 공백으로 구분하여 출력한다.
\( S_1, · · · , S_N\) 및 \(C_1, · · · , C_N\)을 구한 경우
• 첫 번째 줄에 \(1\)을 출력한다.
• 두 번째 줄에 \(S_1, · · · , S_N\)을 공백으로 구분하여 출력한다.
• 세 번째 줄에 \(C_1, · · · , C_N\)을 공백으로 구분하여 출력한다.
입력 예시 Copy
6
1 2 -1
1 3 2
2 4 2
3 5 -3
3 6 -1
출력 예시 Copy
1
5 5 6 8 6 6
3 5 2 0 6 6